Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.3 - Ex. 33

Encontre a transformada de Laplace da função dada. Suponha que é permitido integrar a série infinita termo a termo.

f ( t )   =   1 + ∑ k = 1 ∞ ( - 1 ) k u k ( t )

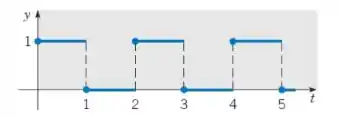
função f ( t )

Passo 1

A transformada de Laplace de uma função f (t) é definida como:

F ( s ) = ℒ { f ( t ) } = ∫ 0 ∞ e - s t f ( t ) d t

Passo 2

Sabemos que, para que essa integral convirja, é necessário que s > 0 . Substitua a função fornecida por f ( t ) , substituindo u k ( t ) pela função Heaviside H ( t - k ) .

F ( s ) = ∫ 0 ∞ e - s t 1 + ∑ k = 1 ∞ ( - 1 ) k H ( t - k ) d t = ∫ 0 ∞ e - s t d t + ∫ 0 ∞ e - s t ∑ k = 1 ∞ ( - 1 ) k H ( t - k )   d t

F ( s ) = ∫ 0 ∞ e - s t   d t + ∑ k = 1 ∞ ( - 1 ) k ∫ k ∞ e - s t d t

Resolvendo as integrais, chegamos em:

F ( s ) = 1 s 1 + ∑ k = 1 ∞ ( - e - s ) k = 1 s ∑ k = 0 ∞ ( - e - s ) k = 1 s 1 1 - ( - e - s ) = 1 s ( 1 + e - s )

Resposta

F ( s ) = 1 s ( 1 + e - s )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dosproblemas de 1a6, esboce o gráfico da função dada no intervalo t≥0 . g ( t )=t - 3 u 2 ( t )– ( t - 2 ) u 3 ( t )
Em cada um dosproblemas de 7a12:(a) Esboce o gráfico da função dada.(b) Expressef ( t ) em termos da função degrau unitário u c ( t ) . f t = t 2 ,0 ≤ t2 1 ,t ≥ 2
Em cada um dosproblemas de 1a6, esboce o gráfico da função dada no intervalo t≥0 . g ( t )=u 1 ( t )+2 u 3 ( t )–6 u 4 ( t )
Suponha que F ( s )=£ { f ( t ) } existe para sa≥0 .(a)Mostre que, se c for uma constante positiva, então L f c t = 1 c F s c ,sc a Suponha que F ( s )=£ { f ( t ) } existe para sa≥0 .(b)Mostre que, s
Em cada um dosproblemas de 1a6, esboce o gráfico da função dada no intervalo t≥0 . g t =f t - 1 u 2 t ,e mq u ef t = 2 ⁡ t