Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 36

Use as séries de Maclaurin da Tabela 1 para obter a série de Maclaurin para a função dada.

f x = s e n π x 4

Passo 1

Eai meus queridos! Tudo na paz!? Bora lá!?

Vamos entender o enunciado. O que a questão pede? Descobrir a série de Maclaurin para a função fornecida f x = s e n π x 4 .

E agora, como faço isso? Bom, primeiro precisamos verificar a forma da série de Maclaurin para a função fornecida. Aí sim, podemos começar a manipular e chegar em uma resposta.

Vamos avaliar a Tabela 1, conforme recomendação:

Observe que tem várias funções e suas respectivas series de Maclaurin, certo!? Vamos verificar se tem alguma parecida.

Opa, temos a seguinte equação:

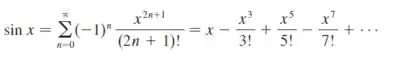
Passo 2

Achamos uma série parecida, porém a equação fornecida no enunciado não é s e n   x , e sim s e n   π x 4 , e agora?

Agora vamos substituir onde tem x por π x 4 e fazer as manipulações para simplificar:

sen ⁡ x = ∑ n = 0 ∞ - 1 n . x 2 n + 1 2 n + 1 !

Dessa forma, a série de Maclaurin fica:

s e n π x 4 = ∑ n = 0 ∞ - 1 n . π 4 x 2 n + 1 2 n + 1 !

s e n π x 4 = ∑ n = 0 ∞ - 1 n . π 2 n + 1 4 2 n + 1 2 n + 1 ! . x 2 n + 1

Resposta

∑ n = 0 ∞ - 1 n . π 2 n + 1 4 2 n + 1 2 n + 1 ! . x 2 n + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a série de Taylor em x = 0 para as funções nos Exercícios 57-64.58. 1 1 + x 3
Cada uma das séries nos Exercícios 51-56 é o valor da série de Taylor em x = 0 de uma função f ( x ) em um ponto em particular. Qual função e qual ponto? Qual é a soma da série? 55. 1 + ln ⁡ 2 + ln ⁡
Cada uma das séries nos Exercícios 51-56 é o valor da série de Taylor em x = 0 de uma função f ( x ) em um ponto em particular. Qual função e qual ponto? Qual é a soma da série? 52. 2 3 - 4 18 + 8 81
Encontre a série de Taylor em x = 0 para as funções nos Exercícios 57-64.59. sen ⁡ π x
Nos Exercícios 41-50, (a) encontre o raio e o intervalo de convergência da série. Em seguida, identifique os valores de x para os quais a série converge (b) absolutamente e (c) condicionalmente42. ∑ n