Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 42
Use um sistema de computação algébrica para determinar o volume exato do sólido.
Entre os paraboloides e e dentro do cilindro .
Passo 1
Fala, galera! Como estão?
A questão pede para usarmos um software para calcular o volume do sólido limitado pelas regiões:
Entre os paraboloides e e dentro do cilindro .
O que vamos fazer aqui é montar a integral:
O que vamos precisar encontrar aqui é e os limites de integração da região .
Daí jogamos num software, como o WolframAlpha, essa integral e ela nos retornará o valor exato do volume .
Vamos pra resolução!
Passo 2
Vamos começar tentando encontrar os limites de integração da região . O domínio de integração é a região dentro do círculo de raio centrado na origem, isto é, .
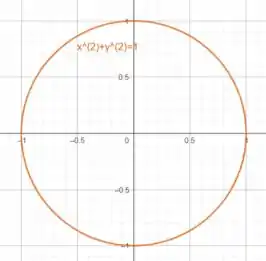
Em coordenadas cartesianas essa região é descrita como:
Passo 3
Agora vamos entender qual a função vai descrever nosso volume.
Temos dois sólidos: os paraboloides
e
Plotando essas equações:
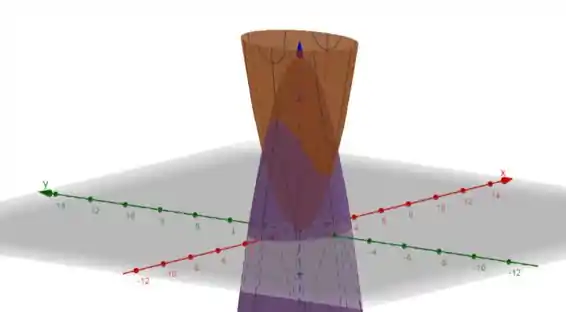
Em roxo temos e em alaranjado temos .
Dessa forma, vamos conseguir o volume total fazendo o volume de um sólido menos o volume do outro. Então podemos escrever nossa função do volume como:
Assim, o volume é dado por:
Veja que colocamos como integral de dentro a integral , já que depende de em seus limites de integração.
Portanto:
Fazendo a integral exata usando uma calculadora gráfica, temos: