Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 41
Use um sistema de computação algébrica para determinar o volume exato do sólido.
Delimitado por e .
Passo 1
Faala, tudo certo?
Bom, essa questão pede pra gente calcular o volume de um sólido!
Pra isso, vamos lembrar que o sólido abaixo do gráfico de é calculado pela integral:
Então o que vamos fazer é encontrar quem é e , e escrever esse volume como uma integral.
No final, vamos usar um sistema de computação algébrica pra calcular essa integral. Eu vou usar o WolframAlpha, mas pode usar o que você preferir!
Passo 2
O nosso sólido está entre as superfícies
A superfície é o plano , então esse sólido vai ser a região abaixo da superfície . Vamos desenhar essa superfície:
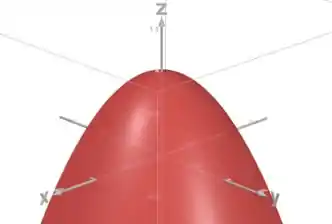
Ela é um paraboloide.
Mas queremos só a região entre ela e o plano , então vamos pegar só a parte do paraboloide acima desse plano:
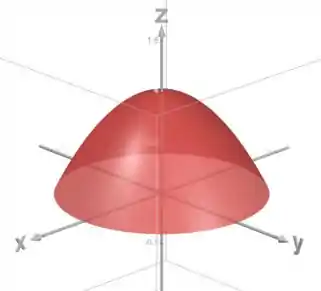
Então, o volume do sólido vai ser a integral desse paraboloide:
Falta descobrirmos quem é .
Passo 3
A região é o domínio dessa parte do paraboloide no plano .
A interseção dessa superfície com o plano é calculada assim:
Isso dá uma circunferência:
Vamos desenhar isso no plano:
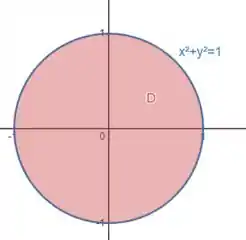
Essa região em vermelho é exatamente a região embaixo do paraboloide, esse vai ser nosso domínio!
Pra expressar isso como uma região do tipo I, vamos reescrever essa circunferência como uma função de , isolando :
A primeira equação é da parte da circunferência acima do eixo (), e a segunda é a parte debaixo ():
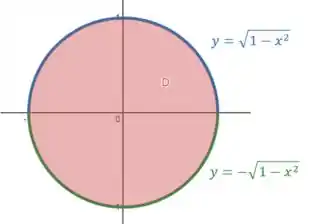
Ou seja, definimos com:
E o volume fica:
Passo 4
Por último, com a ajuda do WolframAlpha vamos calcular essa integral:
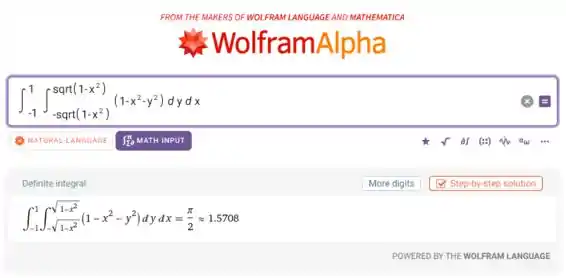
Então: