Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 42

Use um sistema de computação algébrico para determinar o volume exato do sólido.

Delimitado por z = x 2 + y 2 e z = 2 y .

Passo 1

E ai pessoal, beleza? Vamos gabaritar essa!!

Utilizando de um sistema de computação algébrico devemos calcular o volume exato de um solido. Este sólido está delimitado por:

z = x 2 + y 2

z = 2 y

E agora? Como resolvo essa.

Vamos lembrar primeiro da integral de volume:

V = ∬ D z ( x , y ) d A

Onde, z ( x , y ) é a função que delimita a região, d A = d x d y e D é nossa região de integração.

Precisamos montar nossa integral de volume, porém antes vamos fazer um esboço gráfico para sabermos qual função de z ( x , y ) está acima e abaixo da região. Então, podemos fazer:

z x , y = z a c i m a - z a b a i x o

Para encontrar nossa região D , que compreende os intervalos de integração. Vamos igualar as duas equações dadas em z , e observe que a expressão vai ficar com a cara de um circulo com centro deslocado em y . Aqui conseguimos determinar o intervalo do raio r e do ângulo θ .

Como se trata de um círculo, podemos escrever em coordenadas polares:

x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Para resolver a integral, você pode usar a calculadora online WolframAlpha.

Vamos nessa!!!

Passo 2

Vamos começar esboçando as regiões, para tentar visualizar nossa região.

z = x 2 + y 2

z = 2 y

Utilizando o Geogebra, obtemos:

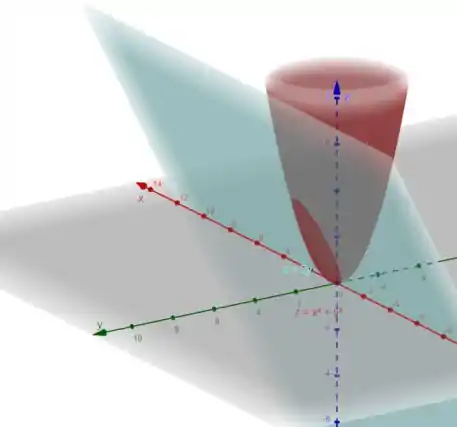
Observe que nossa região esta entre o paraboloide vermelho e o plano. Logo temos que:

z x , y = z a c i m a - z a b a i x o

z x , y = 2 y - x 2 - y 2

Escrevendo em coordenadas polares:

x = r cos ⁡ θ

y = r   s e n   θ

Sabemos que s e n 2 θ + cos 2 ⁡ θ = 1 . Logo temos:

z r , θ = 2 r s e n   θ - r 2

Passo 3

Para identificar o domínio de integração, vamos igualar as funções do paraboloide e do plano. Assim,

x 2 + y 2 = 2 y

Observe que podemos completar quadrado no termo y , adicionado + 1 - 1 :

x 2 + y 2 - 2 y + 1 - 1 = 0

Manipulando, vamos ter a expressão de um círculo de raio 1 deslocando no eixo y .

x 2 + ( y - 1 ) 2 = 1

Fazendo o gráfico do círculo, vamos ter que:

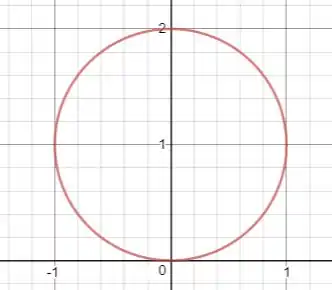
Assim, o domínio de integração é:

D = r , θ ∈ R 2     0 ≤ y ≤ 1 ,     0 ≤ θ ≤ 2 π }

Assim, o volume vai ficar:

V = ∫ 0 2 π ∫ 0 1 2 r s e n   θ - r 2   r d r d θ

Passo 4

Agora precisamos utilizar um sistema de computação algébrico para determinar o volume:

V = ∫ 0 2 π ∫ 0 1 2 r s e n   θ - r 2   r d r d θ

Fazendo a integral exata usando a calculadora online Wolfram Alpha.

Através do input: Integrate[Integrate[2r^2senθ - r^3,{r,0,1}],{θ,0,2π}].

Obtemos:

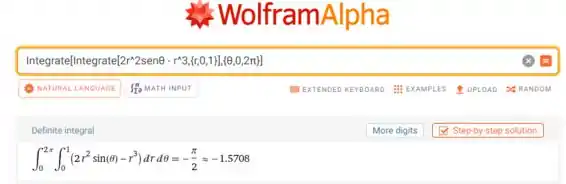
Repare que deu negativo, mas não tem problema. Como estamos calculando volume, não faz sentido considerarmos um volume negativo.

Logo, nosso volume será:

V = π 2

Resposta

π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 - x 1 - x - y d y d x
Encontre a área da superfície com precisão de quatro casas decimais, expressando a área em termos de integral de função de uma variável real e use sua calculadora para estimar a integral.A parte da su
Determine a área da superfície.A parte da esfera x 2 + y 2 + z 2 = a 2 que está dentro do cilindro x 2 + y 2 = a x .
Encontre a área da superfície com precisão de quatro casas decimas, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A parte da superfície z = e
Determine a área da parte finita do paraboloide y = x 2 + z 2 limitado pelo plano y = 25 . [Sugestão: Projete a superfície sobre o plano x y ].