Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 3
(a) Use uma soma de Riemann com para estimar o valor de , onde . Tome os pontos de amostragem como os cantos superiores direitos.
(b) Use a Regra do Ponto Médio para dar uma estimativa da integral do item (a).
Passo 1
Faaala, beleza?
Nessa questão a gente precisa calcular duas vezes a mesma integral!
Ue... como assim??
Bom, a gente vai usar a soma de Riemann pra aproximar o valor da integral:
O que vai mudar da letra (a) pra (b) é que em uma a gente vai usar os cantos superiores direitos como ponto de amostragem – que são os pontos –, enquanto na outra vamos usar os pontos bem no meio de cada partição (essa segunda é a regra do ponto médio!)
Os dois vão ser aproximações pro valor de , mas provavelmente vão dar valores diferentes, tá?
Então nosso roteiro da questão vai ser assim:
Primeiro vamos construir a região e ver os pontos amostrais de cada partição.
Depois, vamos construir a soma de Riemann que aproxima a integral.
E por fim calcular essa soma.
Vamos fazer isso para a letra (a) e depois para a letra (b).
Passo 2
(a)
Começamos então com a região , que é um retângulo com e . Como , que é a quantidade de partições em , e , que é a quantidade de partições em , a região fica assim:
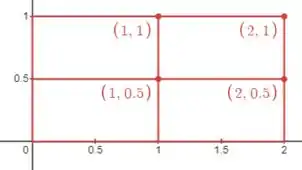
Os pontos superiores direitos de cada uma das partições são nossos pontos amostrais pra calcular a soma de Riemann!
Ou seja, esses pontos marcados no desenho são os que vamos calcular na fórmula:
Lembrando que nossa função é .
O é a área de cada partição:
Vamos às contas:
Passo 3
(b)
Agora vamos fazer de novo a mesma soma de Riemann, mas mudando os pontos amostrais:
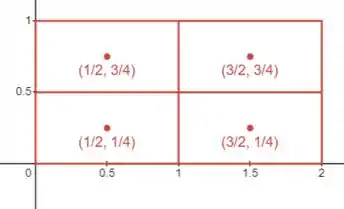
A conta que vamos fazer é:
Mas agora os pontos são os pontos no centro de cada partição, como no desenho.
Só falta fazermos as contas:
E pronto!
Resposta
(a)
(b)