Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 11.11 - Ex. 9
Encontre o polinômio de Taylor da função em . Trace e na mesma tela.
Passo 1
E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Partiuuu!!!! 
Para resolver essa questão, vamos usar o método de séries de Taylor centradas em . Este método é necessário porque estamos lidando com a função , que envolve a multiplicação de uma função linear por uma exponencial.
Primeiro, vamos expandir a função exponencial em sua série de Taylor. Depois, multiplicamos essa série por para obter o polinômio de Taylor resultante de grau .
Vamos usar a série da exponencial, que é uma das funções mais úteis e conhecidas para a expansão em série. A função exponencial tem a seguinte série de Taylor:
Passo 2
Observando nossa função, vemos que podemos usar a série exponencial substituindo por :
Substituindo, temos:
Simplificando os coeficientes, obtemos:
Agora, multiplicamos por :
Passo 3
Para calcularmos , precisamos apenas dos termos de grau 3 e inferiores. Vamos escrever explicitamente os primeiros termos da série:
Portanto, o polinômio de Taylor de grau é:
Passo 4
Vamos traçar as funções e no mesmo gráfico para visualizar a aproximação.
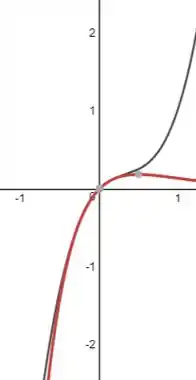
De vermelho temos a função e em cinza .
Resposta
