Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 9a
Utilizando integral dupla, calcule a área do conjunto dado.
Passo 1
Através da integral dupla, tem-se que a área de um conjunto é dada por:
Ou:
Neste caso, é dado no enunciado pela inequação . Observando o esboço do conjunto:
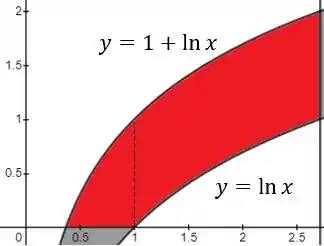
Os limites de integração podem ser dados por:
Tal que o valor de será determinado nesta parte por:
E:
E, para determinar o valor de neste caso:
Passo 2
Logo, a área será dada por:
Resolvendo a integral em relação à :
Substituindo o intervalo de integração:
Sabendo que :
Resolvendo o primeiro termo da segunda integral e fazendo o jogo de sinais do segundo termo:
Sabendo que:
Temos então:
Simplificando os termos semelhantes:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Desenhe um exemplo de uma região que seja Tanto do tipo I quanto do tipo II;Nem do tipo I nem do tipo II.
Desenhe um exemplo de uma região que seja Do tipo I, mas não do tipo IIDo tipo II, mas não do tipo I
Esboce a região de integração e mude a ordem de integração. ∫ 0 2 ∫ x 2 4 f x , y d y d x
Desenhe um exemplo de uma região que seja Do tipo I, mas não do tipo IIDo tipo II, mas não do tipo I
Use a geometria ou simetria, ou ambas, para calcular a integral dupla ∬ D R 2 - x 2 - y 2 d A D é o disco com centro na origem e raio R.