Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 9b
Utilizando integral dupla, calcule a área do conjunto dado.
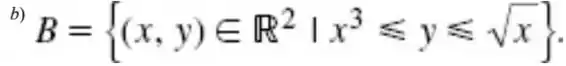
Passo 1
Através da integral dupla, tem-se que a área de um conjunto é dada por:
Ou:
Neste caso, é dado no enunciado pela inequação . Observando o esboço do conjunto:
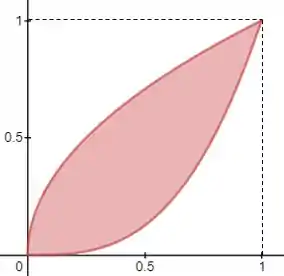
Os limites de integração podem ser dados por:
Tal que o valor de será determinado nesta parte por:
E:
E, para determinar o valor de neste caso:
Passo 2
Logo, a área será dada por:
Resolvendo a integral em relação à :
Substituindo o intervalo de integração:
Passo 3
Agora, integrando em relação à :
Passo 4
Substituindo o intervalo de integração:
Resposta
Exercícios de Livros Relacionados
∫ 0 1 ∫ 0 s 2 cos s 3 d t d s
Calcule a integral dupla. ∬ D y 2 d A D = x , y - 1 ≤ y ≤ 1 ,- y - 2 ≤ x ≤ y }
Determine o volume do sólido dado.Abaixo do plano z = 2 x + y 2 e acima da região limitada por x = y 2 e x = y 3 .
Calcule a integral dupla. ∬ D y 2 d A D é a região triangular com vértices 0,1 , 1,2 , 4,1 .
Uma carga elétrica é distribuída sobre o disco x 2 + y 2 ≤ 1 , de modo que a densidade de carga em x , y é σ x , y = x 2 + y 2 (medida em coulombs por metro quadrado). Determine a carga total no disco