Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 40

Trace a superfície z = x ⋅ s i n ⁡ y , 3 ≤ x ≤ 3 , - π ≤ y ≤ π

e encontre seu comprimento correto com 4 casas decimais.

Passo 1

Vamos lá pessoal, temos que encontrar uma área de uma função z sobre uma superfície qualquer, que segue os seguintes parâmetros:

z = x ⋅ sin ⁡ y , 3 ≤ x ≤ 3 , - π ≤ y ≤ π

Lembre-se que toda vez que precisarmos encontrar isso, devemos utilizar a equação

A s = ∫ ∫ D 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2 ⋅ d A

Que descreve a área sobre uma região D . Agora nós só precisamos especificar corretamente os limites de D e então realizar as derivadas parciais de z em relação a x e y . Vamos tentar?

Passo 2

Temos que a superfície em uma calculadora gráfica fica da seguinte forma

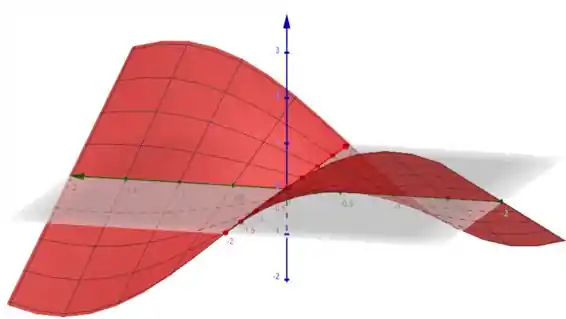
Temos que para a superficie, seu comprimento é dado pela equação da área de uma superficie, que é

A s = ∫ ∫ D 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2 ⋅ d A

Calculando as derivadas parciais, temos então que

∂ z ∂ x = sin ⁡ y

∂ z ∂ y = x ⋅ cos ⁡ y

Passo 3

Substituindo na integral, ficamos com

A s = ∫ ∫ D 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2 ⋅ d A = ∫ - π π ∫ - 3 3 1 + sin 2 ⁡ y + x 2 ⋅ cos 2 ⁡ y ⋅ d x ⋅ d y

Usando um software para calcular essa integral, chegamos que seu valor númerico é

∫ - π π ∫ - 3 3 1 + sin 2 ⁡ y + x 2 ⋅ cos 2 ⁡ y ⋅ d x ⋅ d y ≈ 62.9714

Resposta

A s ≈ 62.9714

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular o volume dos sólidos delimitados pelas superfícies dadas. 1 2 .z = 16 - x 2 - 3 y 2 e z = 4
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 4 .x 2 + y 2 = 1 ,z = 0 e z = x 2 + y 2
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 7 .z = 9 - x 2 - y 2 e z = x 2 + y 2
Calcular o volume do no 1º octante, delimitado por z = 1 - 2 x - 3 y e os planos coordenados.
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 5 .x 2 + y 2 = 4 ,y + z = 8 e z = 0