Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 34
Determine o volume aproximado do sólido no primeiro octante que é limitado pelos planos , e e pelo cilindo . (Utilize uma ferramenta gráfica para estimar os pontos de interseção.)
Passo 1
Oi, pessoal, tudo certo?
Nessa questão precisamos calcular o volume de um sólido!
O volume de um sólido entre o gráfico de uma função e o plano pode ser calculado como:
Onde é o domínio de integração da função.
O que vamos fazer é definir como é esse sólido, pra acharmos quem é e .
Nesse processo, vamos precisar usar uma ferramenta gráfica pra achar os pontos de interseção entre as curvas e conseguir definir o domínio. A que eu vou usar é o desmos, mas você pode usar qualquer uma!
Passo 2
A função que vamos integrar é , que vai ser a “tampa” superior do sólido. A “tampa” inferior é o plano (), na região entre as curvas e . Assim, o volume será a integral:
Vamos esboçar essas superfícies e curvas no primeiro quadrante:
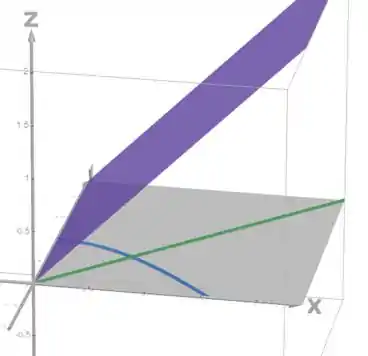
Assim a gente consegue esboçar quem é o sólido:
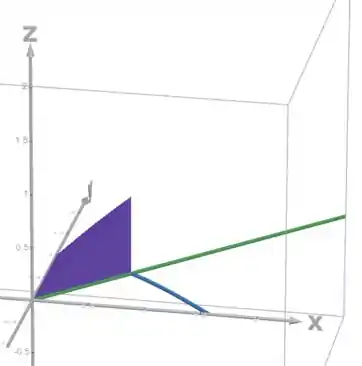
O domínio , então, é essa região:
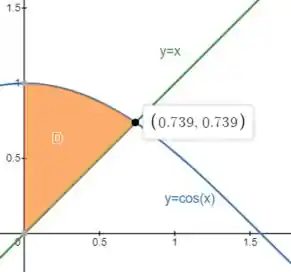
Esse ponto foi calculado pela ferramenta.
Nessa região, o valor de está entre e esse ponto , enquanto o está entre as duas curvas, então:
Ou seja, a integral fica assim:
Agora só falta calcular essa integral!
Passo 3
Primeiro integramos em função de , mantendo constante, então podemos tirar da primeira integral:
Agora podemos resolver normalmente:
Por último, integramos em relação a . Vamos separar em duas integrais:
A primeira integral vamos resolver usando integração por partes:
Então:
Voltando para a integral:
Resolvendo a segunda integral:
Substituindo os valores:
Resolvendo as contas: