Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.2 - Ex. 39
39- Utilize as coordenadas esféricas para achar
Passo 1
As coordenadas esféricas estão relacionadas com as coordenadas cartesianas da seguinte maneira.
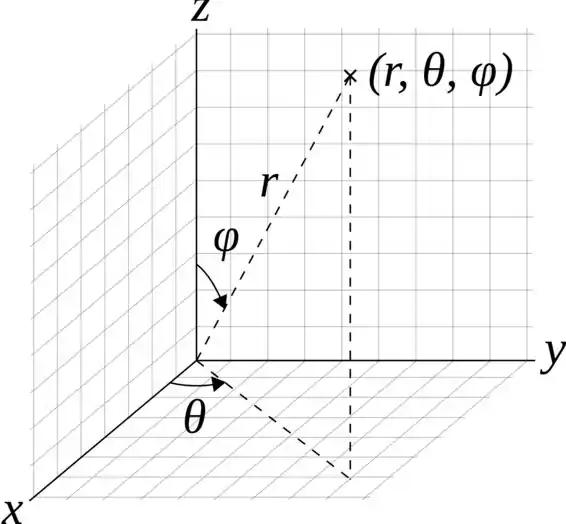
Logo se aplicarmos o limite na quarta equação com nós teremos:
Ou seja o limite será:
Pois e em coordenadas esféricas ditam o comportamento de em coordenadas esféricas. Os ângulos diretores são consequência do tamanho de .
Passo 2
Substituindo e em funções de e e aplicando o limite:
Resposta
Exercícios de Livros Relacionados
Encontre os limites nos Exercícios 13-24 reescrevendo primeiro as frações. lim x , y → 1 ,1 x ≠ 1 x y - y - 2 x + 2 x - 1
Em que pontos ( x ,y ) no plano as funções nos Exercícios 31-34 são contínuas? g x ,y = x 2 + y 2 x 2 - 3 x + 2 g x ,y = 1 x 2 - y
Encontre os limites nos Exercícios 13-24 reescrevendo primeiro as frações. lim x , y → 0 ,0 1 - cos x y x y
Encontre os limites nos Exercícios 13-24 reescrevendo primeiro as frações. lim x , y → 2 ,2 x - y x 4 - y 4
Encontre os limites nos Exercícios 13-24 reescrevendo primeiro as frações. lim x , y → 1 ,- 1 x 3 + y 3 x + y