Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.6 - Ex. 20
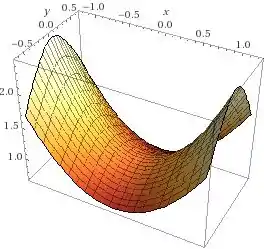
Determine, com precisão de quatro casas decimais, a área da parte da superfície
que está acima do quadrado
Ilustre, traçando o gráfico dessa parte da superfície.
Passo 1
Vamos lá galerinha! Temos uma razão
que representa uma superfície limitada por um quadrado
E precisamos descobrir sua área. O primeiro passo é nos lembrarmos da definição da área de uma superfície qualquer e a partir disso encontrar as derivadas parciais e os limites de integração.
Vamos lembrar que, por definição a área de uma superfície pode ser dada por
Passo 2
Agora que já sabemos o que precisamos calcular, devemos encontrar os limites de integração:
Se:
Então:
Pela definição de módulo:
Sendo de a .
Passo 3
Para encontrar as derivadas parciais temos que fazer:
Utilizando a regra do quociente:
Simplificando:
A derivada parcial em relação a é:
Queremos calcular a área de nossa superfície. Para isso temos que
Usando um sistema de computação algébrica, temos que
Segue a baixo o Gráfico da função
