Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.5 - Ex. 18

Utilize o grafo da árvore para escrever a Regra da Cadeia para o caso dado. Assuma que todas as funções sejam diferenciáveis.

18-

w = f x , y , z ,       o n d e         x = x t , u ,     y = y t , u ,       z = z ( t , u )

Passo 1

E aí, pessoal. Tudo certo?

Nessa questão nós temos a função w = f ( x , y , z ) onde x = x t , u ,     y = y t , u ,       z = z t , u , ou seja, nós temos uma função de três variáveis e essas variáveis dependem de outras duas variáveis.

Parece complexo, né?

Podemos visualizar isso pelo seguinte grafo:

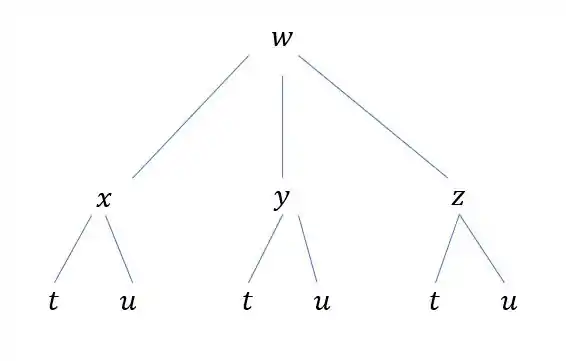
Se quisermos calcular derivadas de w com relação a t e u , precisaremos da regra da cadeia.

Para uma variável, se temos uma função f ( x ) , onde x = x ( t ) , a derivada de f com relação a t é:

d f x d t = d f d x ⋅ d x d t

Como isso funcionaria no caso da nossa questão? Vamos supor que queremos calcular a derivada de w com relação a t .

Veja bem, a função w depende de t   por meio das suas três variáveis ( x , y , z ) , então podemos aplicar o que fizemos para o exemplo de uma variável e somar todas essas parcelas.

Vamos ver como isso é feito agora.

Passo 2

Calculando ∂ w / ∂ t :

Podemos pensar que estamos derivando “de cima para baixo” no grafo. Olha só:

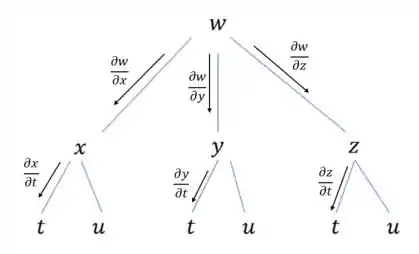
Aí pegamos essas derivadas e somamos, ou seja,

∂ w ∂ t = ∂ w ∂ x ∂ x ∂ t + ∂ w ∂ y ∂ y ∂ t + ∂ w ∂ z ∂ z ∂ t

Passo 3

De forma análoga, fazemos para encontrar a derivada ∂ w / ∂ u :

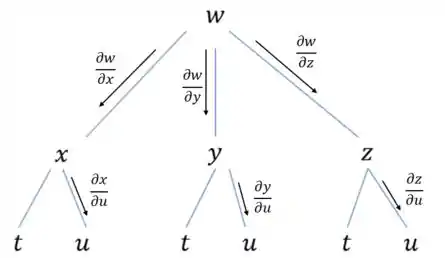
Portanto:

∂ w ∂ u = ∂ w ∂ x ∂ x ∂ u + ∂ w ∂ y ∂ y ∂ u + ∂ w ∂ z ∂ z ∂ u

Resposta

∂ w ∂ t = ∂ w ∂ x ∂ x ∂ t + ∂ w ∂ y ∂ y ∂ t + ∂ w ∂ z ∂ z ∂ t

∂ w ∂ u = ∂ w ∂ x ∂ x ∂ u + ∂ w ∂ y ∂ y ∂ u + ∂ w ∂ z ∂ z ∂ u

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas. z = x 2 + x y 3 , x = u v 2 + w 3 y = u + v e w ∂ z ∂ u; ∂ z ∂ v; ∂ z ∂ w Quando u = 2; v = 1; w = 0
Use a Regra da Cadeia para encontrar a derivada parcial indicada. T = v 2 u + v u = p q r v = p q r ∂ T ∂ p; ∂ T ∂ q; ∂ T ∂ r Quando: p = 2; q = 1; r = 4
Utilize a Regra da cadeia para determinar as derivadas parciais indicadas. R = ln ⁡ u 2 + v 2 + w 2 u = x + 2 y,v = 2 x - y,w = 2 x y ∂ R ∂ x, ∂ R ∂ y Quando x = y = 1 .
Utilize a Regra da cadeia para determinar as derivadas parciais indicadas. M = x e y - z 2 x = 2 u v,y = u - v,z = u + v ∂ M ∂ u; ∂ M ∂ v Quando u = 3,v =- 1
Utilize a Regra da cadeia para determinar as derivadas parciais indicadas. u = x 2 + y z x = p r cos ⁡ θ,y = p r sin ⁡ θ ,z = p + r ∂ u ∂ p; ∂ u ∂ r; ∂ u ∂ θ