Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.5 - Ex. 19

Utilize o grafo da árvore para escrever a Regra da Cadeia para o caso dado. Assuma que todas as funções sejam diferenciáveis.

v = f p , q , r ,       o n d e         p = p x , y , z ,     q = q x , y , z ,           r = r ( x , y , z )

Passo 1

Fala ai galerinha. De boa? A questão pede para determinar a Regra da Cadeia para a função composta v = f ( p , q , r ) onde p , q   e   r   são funções de x , y   e   z .

Especificamente, precisamos encontrar as derivadas parciais de v em relação a x , y   e   z .

Para resolver isso, iremos criar o grafo da árvore para escrever a Regra da Cadeia e depois usaremos a Regra da Cadeia, considerando as dependências de v em p , q   e   r , e de p , q   e   r em x ,   y   e   z .

Vamos começar! 😉

Passo 2

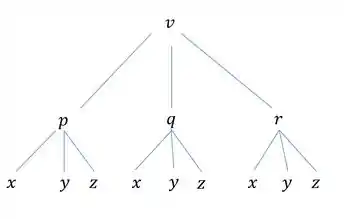
A função v tem três variáveis, logo uma derivada contém três somas. E cada variável pertencente a v possui mais três variáveis fazendo com que v tenha duas derivadas. De modo que tenhamos o seguinte grafo.

Passo 3

As derivadas possíveis são:

∂ v ∂ x = ∂ w ∂ p ∂ p ∂ x + ∂ w ∂ p ∂ q ∂ x + ∂ w ∂ p ∂ r ∂ x

∂ v ∂ y = ∂ w ∂ p ∂ p ∂ y + ∂ w ∂ p ∂ q ∂ x + ∂ w ∂ p ∂ r ∂ y

∂ v ∂ z = ∂ w ∂ p ∂ p ∂ z + ∂ w ∂ p ∂ q ∂ z + ∂ w ∂ p ∂ r ∂ z

Resposta

∂ v ∂ x = ∂ w ∂ p ∂ p ∂ x + ∂ w ∂ p ∂ q ∂ x + ∂ w ∂ p ∂ r ∂ x

∂ v ∂ y = ∂ w ∂ p ∂ p ∂ y + ∂ w ∂ p ∂ q ∂ x + ∂ w ∂ p ∂ r ∂ y

∂ v ∂ z = ∂ w ∂ p ∂ p ∂ z + ∂ w ∂ p ∂ q ∂ z + ∂ w ∂ p ∂ r ∂ z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize a Regra da cadeia para determinar as derivadas parciais indicadas. Y = w tan - 1 ⁡ u v u = r + s,v = s + t,w = t + r ∂ Y ∂ r; ∂ Y ∂ s; ∂ Y ∂ t Quando r = 1 ,s = 0,t = 1
27 – 30 Utilize a Equação 6 para determinar d y / d x .27 – x y = 1 + x 2 y
27 – 30 Utilize a Equação 6 para determinar d y / d x .28 – y 5 + x ² y ³ = 1 + y . e x ² ² ³ ²
27 – 30 Utilize a Equação 6 para determinar d y / d x .29 – cos ⁡ x - y = x e y
27 – 30 Utilize a Equação 6 para determinar d y / d x .30 – sen ⁡ x + cos ⁡ y = sen ⁡ xcos ⁡ y