Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.2 - Ex. 12e
Dê o valor (caso exista) que a função dada deveria ter no ponto dado para ser contínua neste ponto. Justifique.
em
Passo 1
Para uma função ser continua, temos que os limites laterais devem ser iguais, e a função no ponto deve ter o mesmo valor:
Pra começar essa questão, vamos notar o seguinte: seja , não temos como obter esse valor:
Isso porque na expressão de os símbolos são de e , não tendo nenhum , ou . Mas relaxa, sem problema! Pra função ser contínua então, precisamos definir um valor de forma que:
Mãos a obra então!
Passo 2
Não dá pra escolher qualquer e partir pro abraço né? Esse valor tem que fazer sentido. Veja que, pra valores de , quando se aproxima de surgem os seguintes valores de :
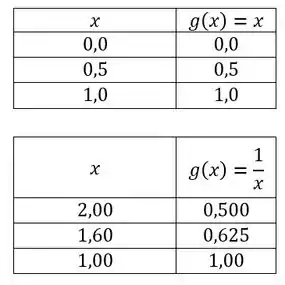
Então, para qualquer valor de , à medida que aproximamos de o valor de se aproxima também de , então esse deve ser o valor da função para que ela seja contínua.
Logo: