Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 06c
A velocidade escalar em t = t1.
Passo 1
Dada da função vetorial da posição
Com isso, a função vetorial da velocidade é sua derivada.
Além disso, o enunciado fornece o dado
Então, podemos descobrir o valor da velocidade no ponto t1 aplicando a função neste instante:
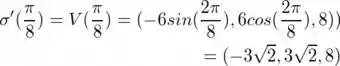
Assim, já temos a velocidade da partícula no tempo solicitado pelo enunciado, porém, na forma vetorial. O enunciado explicita que devemos entregar a velocidade escalar, então, pra isso, precisaremos pegar o módulo desse vetor!
Passo 2
Pra calcular o módulo de um vetor, a gente precisa pegar a raiz quadrada da soma de todos os componentes ao quadrado.
Resposta
Exercícios de Livros Relacionados
Determinar a derivada das seguintes funções vetoriais:d) f → t = e - t i → + e - 2 t j → + k →
Determinar a derivada das seguintes funções vetoriais:f) h → t = 5 t - 2 2 t + 1 i → + ln 1 - t 2 j → + 5 k →
Determinar a derivada das seguintes funções vetoriais:c) h → t = 2 - t i → + t 3 j → - 1 t k →
Determinar a derivada das seguintes funções vetoriais:a) f → t = c o s 3 t i → + t gtj → + s e n 2 tk →
Se r → t é o vetor posição de uma partícula em movimento, mostrar que o vetor velocidade da partícula é perpendicular a r → t .b) r → t = cos 3 t ,s e n 3 t