Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.5 - Ex. 1a
- Verifique quais dos conjuntos a seguir são abertos em
a)
Passo 1
Olá, galerinha! Tudo bom? A primeira coisa que temos que olhar é domínio da função, ou seja, onde ela é valida.
Neste caso o domínio é definido por,
Agora temos que lembrar que figura geométrica essa inequação representa! Então sempre que vermos
Nós temos a equação da circunferência, mas como estamos uma inequação, temos que o domínio é um circunferência cuja o raio máximo sera (mas note que ela não é definida em ).
Passo 2
Graficamente, essa função ficaria,
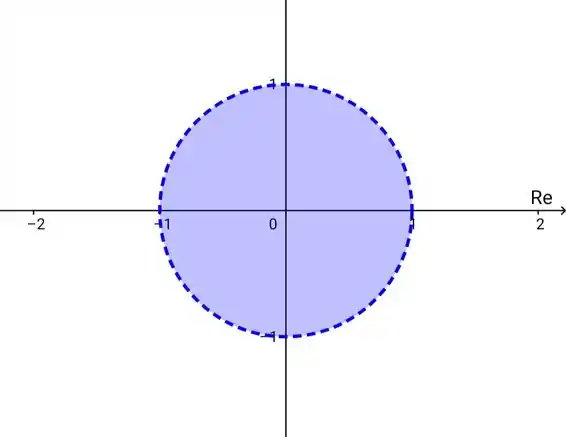
Como tem o pontilhado, significa que o conjunto é aberto.
Resposta
É aberto.
Exercícios de Livros Relacionados
No Exemplo 2 consideramos a função W = f ( T , v ) , onde W era o índice de sensação térmica ocasionado pelo vento, T , a temperatura real e v , a velocidade do vento. A representação numérica foi for
O índice de sensação térmica W discutido no Exemplo 2 foi modelado pela seguinte função: W T , v = 13,12 + 0,6215T - 11,37v 0,16 + 0,3965T v 0,16 Verifique quão próximo este modelo está dos valores da
Suponha que uma curva seja dada pela equação paramétrica x = f ( t ) y = g ( t ) Onde a imagem de f é ( 1,4 ) e a imagem de g é ( 2,3 ) . O que você pode fizer sobre a curva?