Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.8 - Ex. 14
Verifique que o Teorema de Stokes é verdadeiro para o campo vetorial dado e a superfície .
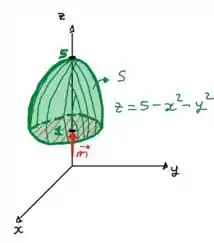
é a parte do paraboloide que está acima do do plano , com orientação ascendente.
Passo 1
Faaala meus queridos, belezinha!?
O problema pede para verificarmos o Teorema de Stokes para o campo:
Onde, a superfície é a parte do paraboloide que está acima do do plano , com orientação ascendente.
A orientação ascendente significa orientada para cima, ou seja, o vetor normal no sentido positivo do eixo. Assim:
O Teorema de Stokes é definido como:
A integral dupla do rotacional de na superfície é igual a integral de linha de ao longo de uma curva fechada .
Para verificar que é verdadeiro, vamos ter que resolver cada integral, e ver se temos a mesma resposta.
Lembre-se que o rotacional é:
E,
Observe que precisamos fazer o determinante para achar o rotacional. Na segunda linha temos as derivadas em relação a , e na terceira linha os respectivos valores do campo vetorial, onde:
Já para a segunda parte da nossa integral, iremos fazer o seguinte:
Repare que precisamos achar uma parametrização para nossa região.
Como temos um paraboloide, logo ele tem uma circunferência na sua base em :
Em , temo um círculo de raio :
A parametrização para um círculo é a seguinte:
Escrevendo em função de , temos que uma parametrização ascendente é:
Agora que está mastigado as informações, deixo o resto com vocês.
Não é complicado, é só organizar as integrais e resolvê-las.
Bora lá!
Passo 2
Vamos calcular primeiro a integral de linha, beleza!
Vimos que uma parametrização para nossa região é:
Para achar , precisamos fazer a derivada de em relação a . Assim:
Precisamos também parametrizar . Assim temos que é:
Substituindo na integral, temos:
Fazendo o produto escalar temos:
A integral do segundo termo será nula pois é uma função trigonométrica periódica integrada em um período completo. Já a primeira vamos fazer uma substituição trigonométrica do tipo:
Assim, ficamos com:
Integrando em , vamos ter:
Aplicando os limites de integração temos:
Logo, concluímos que a integral de linha vale:
Passo 3
Agora vamos fazer a integral de superfície.
Onde,
Antes, precisamos achar o vetor .
O primeiro passo é parametrizar a nossa superfície. Já vimos que temos um círculo em .
Logo,
Substituindo em:
Temos:
Assim, ficamos com:
Pra achar é só fazer as derivadas em relação a e a . Desta forma, vamos ter:
Logo, podemos escrever o produto vetorial como:
Portanto, o modulo vai ser:
Assim,
*O sinal de menos serve para seguir a orientação pedida no enunciado!
Portanto,
Logo,
Passo 4
Agora vamos achar o rotacional de :
Em coordenadas paramétricas, vamos ter:
Assim, substituindo na integral temos:
Fazendo o produto escalar, vamos ter:
Substituindo os intervalos de integração, ficamos com:
Fazendo a integral em , o termo do meio se anula porque vamos ficar com uma integral periódica. Assim ficamos com:
Aqui podemos fazer uma substituição trigonométrica do tipo:
Logo, nossa integral fica:
Passo 5
Vamos separar nossa integral para facilitar, desse jeito:
Agora é só integrar.
Integrando em , vamos ter:
Aplicando os limites, ficamos com:
Observe que a segunda integral vai dar zero, restando apenas a primeira integral.
Integrando em , temos:
Aplicando os limites de integração, vamos ter:
Mas sabemos que
Logo, concluímos que a integral de superfície pelo teorema de Stokes é:
Note que obtivemos o mesmo resultado pelas duas integrais!
Resposta
O teorema de Stokes é verdadeiro!