Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.1 - Ex. 50
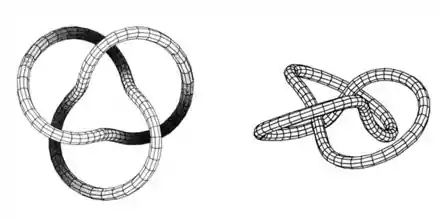
A visão do nó de trevo apresentada na Figura 8 é correta, mas não muito reveladora. Use as equações paramétricas
para esboçar à mão a curva vista de cima, deixando pequenas falhas para indicar os pontos onde a curva se sobrepõe. Comece mostrando que sua projeção sobre o plano tem coordenadas polares e , de forma que varia entre e .
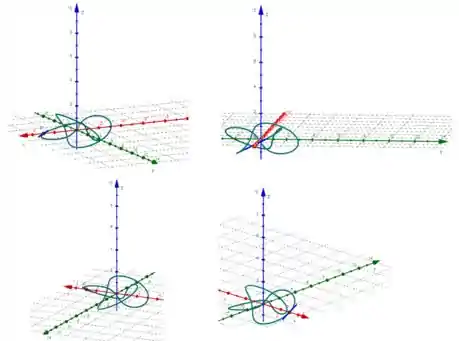
Quando você terminar o esboço �� mão livre, utilize um computador para traçar a curva com o observador vendo de cima e compare-a ao seu desenho. Trace a curva sob outros pontos de vista. Você alcançará melhor resultado se traçar um tubo de raio em torno da curva. (Utilize o comando tubeplot no Maple.)
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu as seguintes equações paramétricas:
Queremos esboçar essa curva vista or cima, ou seja, como se nossos olhos estivessem no eixo .
Além disso, o enunciado quer que comecemos mostrando que sua projeção sobre o plano tem coordenadas polares e , de forma que varia entre e .
Agora bora lá!! 😉
Passo 2
Bom, galera, a projeção da curva no plano é dada pelas equações paramétricas:
Se a gente converter para coordenadas polares, teremos:
Substituindo e :
Sabemos que , logo:
Então,
Passo 3
Além disso, teremos:
Substituindo e :
Então,
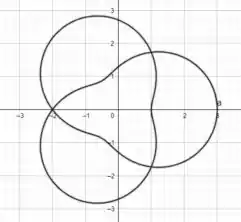
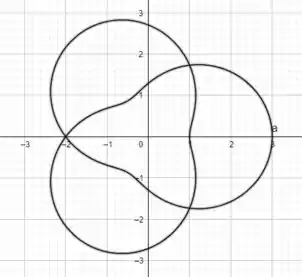
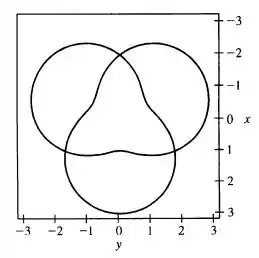
Portanto, a equação polar da curva é , e vai variar entre e .
Se tentarmos fazer um esboço dessa curva, ficará assim:
Passo 4
Nós podemos determinar como a curva passa sobre si mesma investigando os valores máximos e mínimos de .
Já que , será máximo quando:
E será mínimo quando:
Mas note que esses são precisamente os valores que nos dão:
Então tem valor máximo e mínimo quando a projeção está entre e .
Passo 5
Agora, usando um computador, vamos traçar a curva sob várias perspectivas:
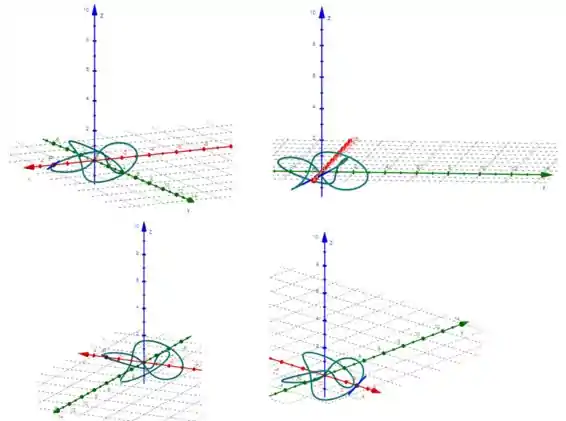
Traçando um tubo de raio em torno da curva, temos:
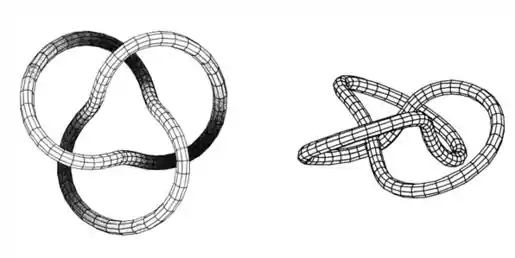
Resposta
