Limite de uma Sequência
Produzido por Carolina SabaTeoria
Fala aí, nós somos o Responde Aí, e estamos aqui pra ajudar você a arrasar nas provas!
Hoje vamos falar sobre Limites de uma Sequência. Está preparado para entender tudo sobre isso agora? Então, bora lá!
Conhecimentos Prévios
Limites de uma Sequência
Dá uma olhada nessa sequência aqui:
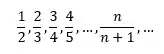
Imagina que a gente quer saber qual é o último termo dessa sequência. Concorda comigo que isso vai depender de até qual valor de
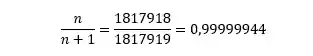
Mas, e se o
Se isso acontece concorda que não existe um último termo para a sequência? Porque se
O que fazemos nesses casos é calcular o limite da sequência quando o
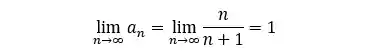
Quando fazemos isso, nós encontramos o valor que os termos tendem quando o
Essa limite de uma sequência nos diz uma coisa bem importante sobre a sequência: se ela é convergente ou divergente.
- Se o limite existe e é igual a um número finito, então a sequência é convergente;
- Se o limite não existe e "estoura" para o infinito, então a sequência é divergente
E aí você me pergunta: "Ahhh, todas aquelas propriedades de limites que usamos para as funções valem aqui também?". Siim, valem, sempre que o termo geral da série puder ser aproximado por uma função contínua, ou seja, a função contínua coincide com a sequência em todos os valores inteiros de
Vamos fazer mais um exemplo pra ficar tudo bem claro, beleza?
EXEMPLO: A sequência com termo geral,
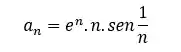
Para saber se a sequência é convergente ou divergente temos que fazer o limite. Então vamos lá:
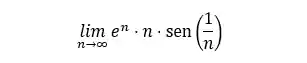
📢ALERTA: Para resolver esse limite teremos que usar algumas propriedades dos limites, alguns limites fundamentais, as vezes até aplicar a regra de L'Hospital, então é uma boa você dar uma revisada nisso. Se preferir pode conferir essa nossa página de assunto: Limites
Resolvendo o limite:
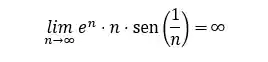
Assim, chegamos a conclusão que a sequência diverge.
De boas não, é? O segredo agora é praticar. E pensando nisso nós temos muito exercícios resolvidos passo a passo. Não deixa de conferir: Exercícios - Limite de uma Sequência
Além de conteúdos em textos, nós do Responde Aí produzimos também conteúdos em vídeos. Se você é uma pessoa que prefere assistir uma boa aula não deixa de conferir o nosso vídeo aqui embaixo 👇🏽 sobre limites de uma sequência 😉
Vídeo
Curtiu nosso conteúdo? Então assine com a gente para ter acesso a muito mais!
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Analise a convergência da sequência, no caso de convergir, calcule seu limite.
Passo 1
Definindo:
Temos:
Passo 2
Vamos calcular o limite:
Lembrando que o limite do produto é o produto dos limites:
No Segundo limite podemos fazer:
Substituindo:
Resposta
Portanto, e a sequência diverge.
Exercício Resolvido #2
UFF - Equações - Lista 1 – 3
Mostre que se a sequência
É convergente.
Passo 1
Vamos calcular o limite quando n tende ao infinito:
Se tivermos então:
Isso significa que conforme o valor de aumenta, os termos da nossa sequência vão se aproximando cada vez mais do valor 1.
Logo,essa sequência converge.
Obs: lembrando que aqui tem que ser positivo por que temos que ter uma base positiva!
Resposta
A sequência converge
Exercício Resolvido #3
UFF - Equações - Lista 1 - 1c
Determine se a seguinte sequência possui limite
Para algum fixado.
Passo 1
Temos que fazer:
Isso é uma indeterminação. Vamos multiplicar pelo seu conjugado
Logo, ele tem limite e esse limite é .
Resposta
Ele tem limite e esse limite é .
Exercício Resolvido #4
UNICAMP - Cálculo 3 - P3 2010.2 - 2ª
Calcule o limite da sequência:
Se ela for convergente.
Passo 1
Vamos escrever a função associada a esta sequência: basta trocar por :
E agora vamos buscar o limite (se convergir). Para isso, temos que analisar .
Passo 2
Esse limite ta complicado de resolver de cara, então vamos reescrever essa função de outra forma para ver se facilita.
Repara que a gente aplicou uma propriedade de potência e chegamos um limite que pode ser resolvido através do limite fundamental exponencial. Lembrando que o limite fundamental é dado como:
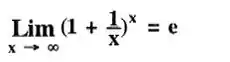
Nesse caso, teremos que:
Fazendo , temos que:
Então agora é só resolver o que está dentro dos colchetes:
Portanto:
Resposta
.
Exercício Resolvido #5
USP - Cálculo 4 - P1 2014 - 1a
Determine se a sequência abaixo é convergente ou divergente, e caso convergente, determine o seu limite:
Passo 1
Uma sequência é convergente quando o limite existe e vale um número. E ela é divergente quando o limite não existe e estoura para o infinito.
Então, para saber se uma sequência converge, basta calcular o seu limite, então fica:
Repara que temos:
Pô várias indeterminações, vamos ter que dar uma arrumada nisso aí.
Passo 2
A primeira coisa que podemos fazer é isso aqui:
Então, temos que:
Passo 3
Agora você precisa lembrar da fórmula do limite fundamental exponencial. Não lembra? Eu te ajudo!
Então, o que a gente vai ter é:
Resposta
Converge e o valor do limite é