Teorema do Resto das Séries Alternadas de Taylor
Produzido por Carolina SabaTeoria
Revisão – Séries Alternadas
Antes de vermos o Teorema das Séries Alternadas, vamos relembrar o que é uma série alternada!
Uma série alternada é aquela em que os termos têm seus sinais alternados, daí que vem o nome! Mas o que isso quer dizer?
Se você tem um termo positivo, o próximo termo é negativo. E se você tem m termo negativo, o próximo é positivo! Vejamos um exemplo de série alternada:
Esta série é conhecida como série harmônica alternada!
Agora que vimos o que é uma série alternada, vamos ver como se dá sua convergência! A convergência de séries alternadas podem ser verificadadas pelos critérios estabelecidos no teorema de Leibniz. Não se assuste!! Vamos ver o teorema de Leibniz já já.
Seja uma série alternada genérica:
O teorema de Leibniz diz que ela vai convergir se as seguintes condições foram satisfeitas:
- Os forem todos positivos.
- para todo , para algum inteiro.
- .
Se a série seguir estes três critérios, então a série converge!
Pronto, acho que já fizemos uma revisão sobre séries alternadas vamos ver o teorema das séries alternadas e como ele pode ser útil para séries de potências!
Teorema da Séries Alternadas
Vamos pegar uma série alternada convergente, ou seja, que satisfaz os três critérios que vimos ali em cima! Agora vamos avaliar como a soma dessa série muda de acordo com o número de termos que estamos pegando!
A soma de termos pode ser defininda como , ou seja:
E vamos chamar:
Observando com atenção a figura
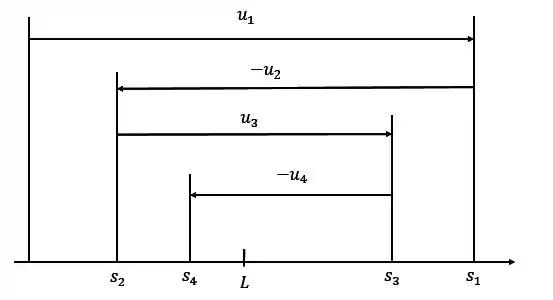
Podemos ver que a soma vai se aproximando de conforme vamos aumentando o valor de ! E que a distância entre a soma parcial( e é menos que o temo .
Essas observações vão ajudar a entender melhor o teorema!
Teorema: Se a série alternada satisfaz as três condições de convergência, então para , se aproxima da soma da série com um erro cujo valor absoluto é menor que , que o valor numérico do primeiro termo a não ser utilizado.
O que isso quer dizer? Que ao aproximar a série :
Fazendo um truncamento com termos, o erro desta aproximação é menor que o primeiro termo deixado de fora! Ou seja,
Além disso, temos que o sinal do erro é o mesmo sinal de na série.
E isso pode ser aplicado para estimar erro de séries de potências alternadas, veja o exemplo!
Exemplo: Encontre a série de Taylor gerada por em e avalie seu erro para aproximando a função com três termos.
Passo 1:
Precisamos encontrar os padrões das derivadas,
Assim,
Passo 2:
A série de Taylor é dada por
Como e temos os valores das derivadas:
Logo temos uma série alternada e podemos avaliar o erro pelo teorema das séries alternadas!
Passo 3:
Vamos calcular algumas somas parciais e ver com elas se aproximam da função!
Pegando três termos da série, temos :
Mas sabemos que,
Então, de acordo com o teorema das séries alternadas, o erro deve ser menor que o quarto termo da série, que é:
Logo, vimos que o teorema dá certo!!
Teorema da Séries Alternadas
Exercícios Resolvidos
Exercício Resolvido #1
George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education do Brasil ltda., 2009, pp. 136-19.
Aproximadamente, para quais valores de você pode substituir por com um erro cuja magnitude não seja superior a ? Justifique sua resposta.
Passo 1
Neste exercício o enunciado já nos da que a função deve estar escrita como série de Maclaurin, então
Que é uma série alternada!
Passo 2
Assim, podemos usar o teorema das séries alternadas para avaliar o erro!
Sabemos, pelo enunciado, que
Pelo teorema das séries alternadas, temos
Assim, devemos ter
Resposta
Para valores de , podemos fazer a aproximação com um erro menor que .
Exercício Resolvido #2
George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education do Brasil ltda., 2009, pp. 136-21.
Quão precisa é a aproximação quando ? Para quais desses valores de ocorrerá de ?
Passo 1
Neste exercício o enunciado já nos da que a função deve estar escrita como série de Maclaurin, então
Que é uma série alternada!
Passo 2
Assim, podemos usar o teorema das séries alternadas para avaliar o erro!
Pelo teorema das séries alternadas, temos
Sabemos, pelo enunciado, que
Assim, devemos ter
Passo 3
Quermos encontrar os valores de para , então vamos tentar relacionar isso com o erro da série!
Substituindo
Temos,
Queremos encontrar os valores para os quais,
Passo 4
Agora vamos encontrar os valores de que nos dão o resto positivo!
O resto tem o mesmo sinal do primeiro termo da série a ser cortado, ou seja, o mesmo sinal de
Esse termo somente é positivo para
Como ,
Resposta
Quando , pode ser aproximado por com precisão de
E para , temos que .
Exercício Resolvido #3
George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education do Brasil ltda., 2009, pp. 136-28.
Você planeja estimar pela determinação da série de Maclaurin para em. Use o teorema da estimação de séries alternadas para determinar quantos termos da série você tem de adicionar para ter certeza de que a estimativa tem precisão de duas casas decimais.
Passo 1
Neste exercício o enunciado já nos dá que a função deve estar escrita como série de Maclaurin, então
Que é uma série alternada!
Passo 2
Assim, podemos usar o teorema das séries alternadas para avaliar o erro!
Sabemos, pelo enunciado, que a aproximação deve ter precisão de duas casas decimais, logo
Como, pelo teorema,
Então devemos ter, para
Resposta
O resultado nos diz que para a precisão pedida, devemos pegar mais que termos!