Forma Matricial de um Sistema de EDO’s
Teoria
Fala aí, seja muito bem vindo ao Responde Aí! Hoje a gente vai aprender como resolver um sistema de EDOs usando a forma matricial e também como passar um sistema de EDOs para a forma normal!
Mas antes de qualquer coisa…O que é um sistema de EDOs?! 😖
Um sistema de EDOs tem essa carinha aí de cima e ele é um sistema com EDOs de primeira ordem que envolvem variáveis dependentes (
📢 Clique para saber mais:
- Forma Matricial de um Sistema de EDOs: Exercícios Resolvidos
- Método Matricial – Caso Homogêneo
- Método Matricial – Caso Não Homogêneo
Agora bora aprender como escrever o sistema de EDOs para a forma matricial?!
Forma Matricial
Passar o sistema de EDOs para forma matricial é muito mais fácil do que parece, e eu vou te mostrar como! Pra isso vamos pegar o sistema de EDOs que a gente viu lá em cima:
A forma matricial segue a seguinte lógica:
Onde
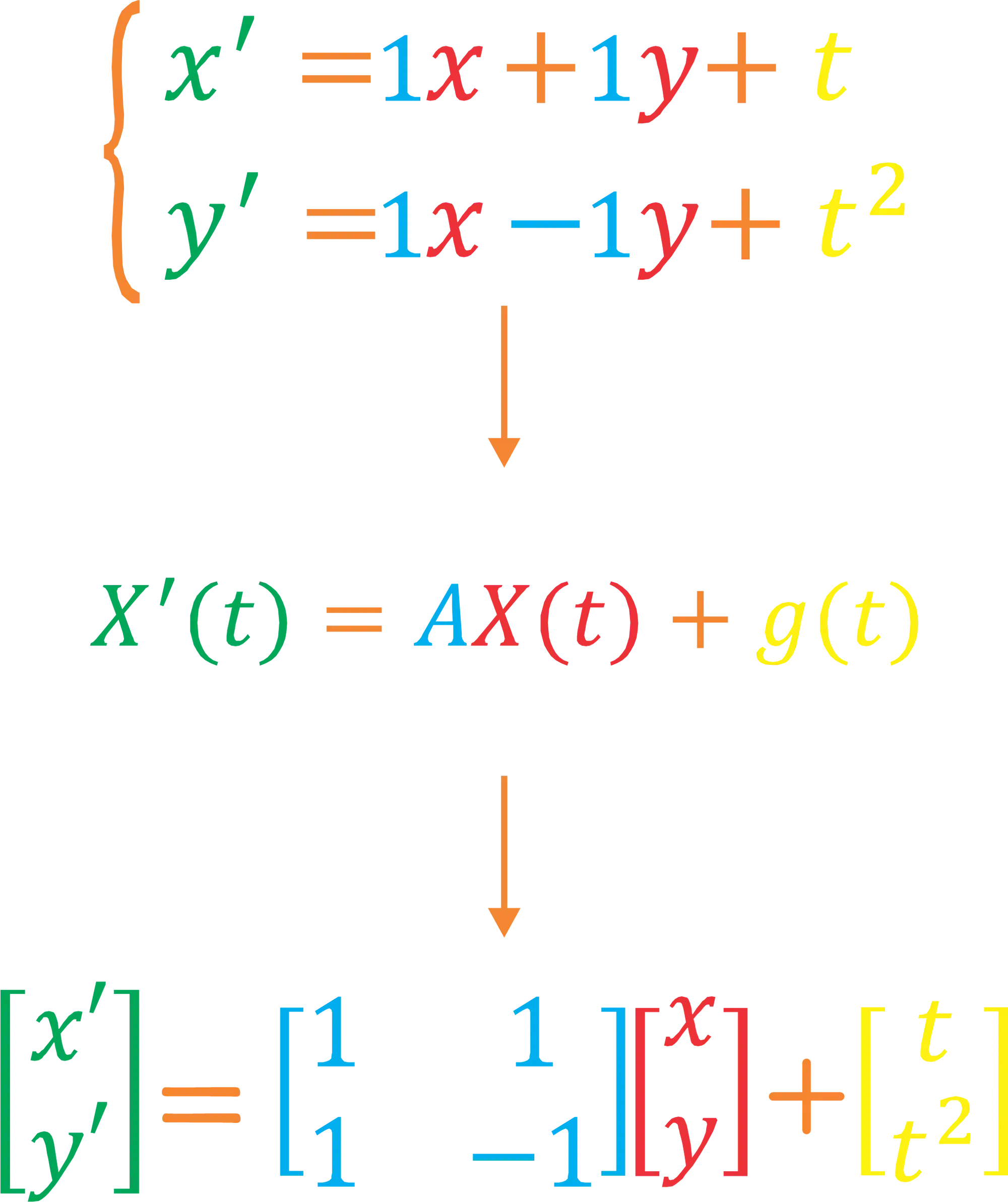
-Beleza, mas e nos exercícios e na prova…como isso cai?! 😖
Excelente pergunta! A gente preparou um vídeo completaço pra você ficar fera em Sistemas de EDOs! Se liga 👇👇👇
Como passar um sistema de EDOs para a Forma Normal
Na forma normal de uma EDO só aparecem derivadas de primeira ordem, facilitando e muito a resolução delas! Agora vamos ver o passo a passo de como passar um sistema de EDOs para a forma normal. Se liga nesse exemplo:
Passo 1: Passar as derivadas de maior ordem para um lado da equação e o resto para o outro
Reorganizando nosso sistema, ficamos com:
Passo 2: Escrever cada equação em função de somente uma das derivadas de maior grau
Fazendo isso ficamos com:
Passo 3: Escrever a derivada de maior grau em função das variáveis criadas
Agora vamos fazer a mudança de variável. Como o grau máximo é 2 temos que fazer uma mudança de variável com as derivadas de ordem 1. Sendo assim.
Vamos agora calcular as derivadas de ordem 2, maior ordem, em função das mudanças de variável.
Passo 4: Montar o sistema na forma normal
E finalmente temos:
Sistema Degenerado
Um sistema degenerado é um um sistema de equações que não possa ser escrito na forma normal. Isso ocorre quando ao tentarmos eliminar algumas derivadas de uma das equações eliminamos todas. Vamos analisar um exemplo
Vamos tentar remover o termo
Como foi impossível escrever a segunda equação somente em função de
Por hora é isso pessoal, agora vamos praticar com exercícios?!
Como passar um sistema de EDOs para a Forma Normal
Sistema Degenerado
Exercícios Resolvidos
Exercício Resolvido #1
Dennis Zill, Equações diferenciais volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2006, pp25-1
Escreva a equação diferencial dada como um sistema na forma normal.
Passo 1
Para resolver essa problema temos que primeiro identificar a variável de maior ordem e colocar somente ela de um lado. No nosso problema a derivada de maior ordem é .
Passo 2
Como a EDO é de segunda ordem, só precisamos de uma nova variável que vai ser da forma
Derivando em função de .
Passo 3
Como já escrevemos as derivadas em função da nossa nova variável podemos montar o sistema na forma normal.
Resposta
Exercício Resolvido #2
Dennis Zill, Equações diferenciais volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2006, pp25-12
Escreva, se possível, o sistema dado na forma normal.
Passo 1
A forma normal de uma EDO é essa forma como o enunciado apresentou a EDO, com o sistema e as derivadas de segunda ordem no mesmo lado. Agora, vamos escrever cada equação em função de somente uma derivada de segunda ordem.
Para fazermos isso, é como se nós estivéssemos resolvendo um simples sisteminha de equações para as variáveis e .
Resolvendo esse “sisteminha” isolando os termos e , ficamos com o seguinte sistema:
Passo 2
Chamando cada derivada de primeira ordem de uma nova variável.
Derivando as equações em função de
Passo 3
Como já escrevemos as derivadas em função das nossas novas variáveis podemos montar o sistema na forma normal.
Resposta
Exercício Resolvido #3
Dennis Zill, Equações diferenciais volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2006, pp25-13(Modificado)
Escreva, se possível, o sistema dado na forma normal.
Passo 1
A derivada de maior ordem é a derivada de ordem um, vamos reescrever o sistema de forma a deixar essas derivadas de um lado das equações e as demais funções do outro.
Dividindo a primeira equação por 2.
Passo 2
Se tentarmos remover ou de alguma das equações vamos perceber que é impossível remover um sem remover o outro, logo, o sistema trata-se de um sistema degenerado e não pode ser escrito na forma normal.
Resposta
O sistema é um sistema degenerado e não pode ser escrito na forma normal.