de uma substância contida em um tanque rígido é colocada em contato com uma fonte térmica de fluxo . O gráfico do aquecimento em função do tempo é apresentado. Determine o calor específico a volume constante da substância. Suponha que não exista variações de energias cinética e potencial da substância.
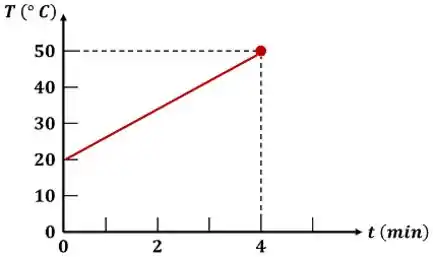
Passo 1
Sabemos que o calor específico a volume constante é a derivada parcial da energia interna específica em relação à temperatura , mantendo o volume específico constante. Ou seja, para calcular o valor de precisamos saber como varia em função de , enquanto permanece constante.
Mas em que parte do enunciado em função de é informado?

A forma que varia com é dada indiretamente pelo enunciado.
Mas antes, para entender como essa informação está escondida no texto do problema, precisamos entender todos os dados que o enunciado mostrou pra gente. Por exemplo, o que é o fluxo de da fonte térmica?

Ele é a quantidade de calor que a substância recebe a cada segundo! Logo, para saber quanto a substância ganha de calor depois de ficar um tempo em contato com a fonte, devemos fazer regra de três! Nós vamos usar o símbolo para representar essa variável em uma fórmula.
onde é o tempo em que o tanque está em contato com a fonte térmica. Ele está em segundos .
O problema diz que:
Mas qual a conexão de com a variação de energia interna específica ?
Descobriremos isso no próximo passo!
Passo 2
Essas duas variáveis se conectam através da primeira lei da termodinâmica!
onde:
- é a variação de energia cinética da substância. Ela vale zero segundo o enunciado;
- é a variação de energia potencial da substância. Ela vale zero segundo o enunciado;
- é a massa da substância. Ela vale segundo o enunciado.
- é o trabalho realizado pela substância;
- é a variação de energia interna específica antes e depois do aquecimento. Ela faz parte da incógnita do problema.
Para descobrirmos , precisamos saber calcular o trabalho . No entanto, o seu valor é dito indiretamente pelo enunciado!
Como o texto não fala nada sobre uma realização trabalho de eixo durante o processo de aquecimento, essa possibilidade é descartada.

Além disso, o texto fala que a substância está contida em um tanque rígido. Isso significa que o volume da substância permanece o mesmo durante todo o aquecimento! Ou seja, não existe movimento de fronteira nem trabalho de movimento de fronteira! Por conta de tudo isso, o trabalho vale:
Depois de todas essas observações, precisamos reorganizar a primeira lei para encontara .
Já descobrimos uma fórmula de em função do tempo , mas, para calcular , precisamos de uma fórmula de em função da variação de temperatura . Como podemos chegar onde queremos?
Isso será mostrado mais pra frente. Antes, temos que ter certeza que a fórmula de conseguimos mostra a variação de para volume específico constante.
Passo 3
Para saber se as substância está ganhando energia, mas mantendo seu volume específico constante, temos que descobrir outra informação que está escondida no texto da questão!

A questão nos diz que a substância está contida em um tanque rígido. Isso significa que o seu volume não varia conforme ela é aquecida! Além disso, a massa () da substância também não varia durante o aquecimento.
O volume específico é igual ao volume dividido pela massa. Como os dois são constantes, o volume específico também é constante no aquecimento do problema!
Isso mostra que a informação presente no gráfico pode ser usada para calcular os , porque é constante durante o aumento de !
Passo 4
Para achar em função de , precisamos descobrir uma fórmula de em função de e depois substituir na fórmula de !

Isso é mostrado no gráfico. Através dele, vemos que em função de é uma reta. Logo, podemos descobrir uma fórmula para essa reta através de dois pontos. O primeiro ponto pode ser o início do aquecimento e o segundo ponto pode ser no tempo de quatro minutos.
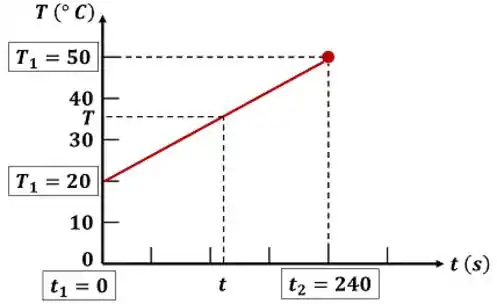
A inclinação da reta é constante, logo:
onde:
Reorgazinando a fórmula para , encontramos:
Substituindo essa fórmula na equação de , achamos:
Mas a variação da energia interna específica também pode ser calculada como a diferença entre a energia interna específica durante o aquecimento e a energia interna específica no início do aquecimento .
Substituindo isso na fórmula encontramos que:
Não conhecemos , mas ele é uma constante. Isso quer dizer que esse termo vai desaparecer, quando derivarmos .
Pronto, temos a fórmula de . Então vamos derivá-la no próximo passo para podermos calcular .
Passo 5
Derivando em relação à temperatura , achamos:
Ou seja:
Com isso a gente pode substituir todos os valores que conhecemos e achar .