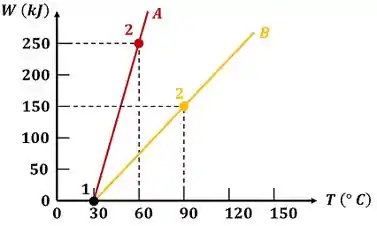
Considere que uma fábrica possui dois conjuntos cilindro-pistão. Cada um deles contém uma única substância. O conjunto cilindro-pistão contém da substância e o conjunto cilindro-pistão contém da substância . Os conjuntos cilindro-pistão realizam um processo adiabático de enpansão. O gráfico mostra a quantidade de energia perdida por trabalho pelas duas substâncias em função da temperatura. Suponha que o processo de expansão das substâncias e é isobárico a de pressão. Determine o calor específico a pressão constante das duas substâncias.
Passo 1
O enunciado fala sobre dois cilindros-pistões e , cada um com uma substância. Eles realizam trabalho. A quantidade de trabalho que as substâncias realizam está mostrada no gráfico. A partir dessas informações, a questão pede pra gente calcular o calor específico a pressão constante das duas substâncias. Os dados e as incógnitas do problema estão ilustrados pela figura abaixo. Será explicado o significado de cada dado mostrado na figura!
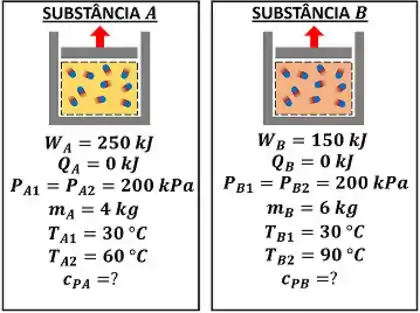
Para conseguir calcular o calor específico a pressão constante das duas substâncias, precisamos lembrar da única fórmula que temos pra isso. Ela é a derivada parcial da energia interna específica em relação à temperatura , mantendo o pressão da substância constante. Ou seja, é taxa de variação da entalpia específica em relação à temperatura.
Isso quer dizer que para calcular precisamos de informações sobre a variação de , mantendo a pressão constante. Para conseguir esses dados, temos que usar a primeira lei. Com ela encontraremos informações sobre a variação da energia interna específica a pressão constante. Isso é obtido, aplicando a primeira lei nessas duas substâncias ( e ).
O significado de cada variável da primeira lei será explicado no próximo passo.
Passo 2
e são as massas das substância e respectivamente. O enunciado informa todos os valores de massa. Todos eles estão presentes na figura acima!
e são as variações de energia interna específica das substância e respectivamente. Elas são importantes de serem calculadas, porque vão ajudar no cálculo dos ’s. Elas são as variações que as substâncias sofrem ao ir do ponto ao ponto .
e são os calores trocados pelos tanques e com o ambiente. Todos os dois valem zero, porque o enunciado informa que o processo de expansão é adiabático.

Com esses dados, podemos calcular as variações de energia interna específica , reorganizando a primeira lei.
Mas a entalpia específica pode ser calulada a partir da energia interna .
onde é a pressão da substância e é o volume que a substância ocupa.
Podemos usar essa fórmula para calcular a variação de entalpia específica das duas substâncias!
As pressões e são as pressões das substâncias no ponto e as pressões e são as pressões das substâncias no ponto . As pressões do ponto são iguais às pressões do ponto , porque o processo de compressão é isobárico. Elas são mostradas na figura.
Os volumes e são as pressões das substâncias no ponto e os volumes e são as pressões das substâncias no ponto . e serão calculados no próximo passo.
Passo 3
Os trabalhos de expansão e são trabalhos de movimento de fronteira à pressão constante. Como conhecemos a fórmula de trabalho de movimento de fronteira isobárico, podemos calcular e a partir dela.
Substituindo e nas equações de variação de entalpia específica, encontramos:
Vemos que as variações de entalpia específica dependem da quantidade de trabalho realizado . Perceber isso é muito importante, porque a quantidade de trabalho varia linearmente. Como a variação de depende de , também varia linearmente. Por isso, o calor específico pode ser calculado da seguinte forma.
Vemos pelo gráfico que as temperaturas das substâncias no ponto são iguais a .
Já as temperaturas dos pontos estão mostradas na figura!
Com todos esses dados, podemos enfim calcular os calores específicos!
Passo 4
Enfim, encontramos o que a gente queria!