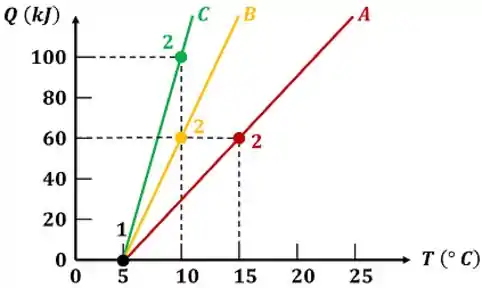
Considere que uma fábrica possui três tanques rígidos. Cada um dos três tanques rígidos contém uma única substância. O tanque contém da substância , o tanque contém da substância e o tanque contém da substância . Os três tanques são aquecidos separadamente. O gráfico fornece a quantidade de calor absorvida pelas três substâncias em função da temperatura. Determine qual é a substância com o menor calor específico a volume constante.
Passo 1
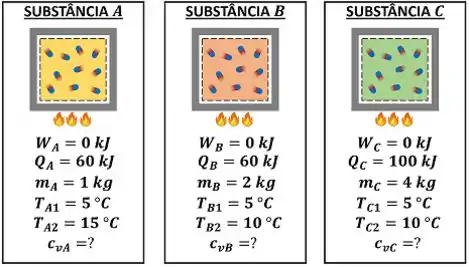
O enunciado fala sobre três tanques rígidos, cada um com uma substância. Eles são aquecidos e a quantidade de calor que as substâncias recebem está mostrada no gráfico. A partir dessas informações a questão pede pra gente calcular o calor específico a volume constante das três substâncias. Os dados e as incógnitas do problema estão ilustrados pela figura abaixo. Depois da figura, será explicado como cada dado foi obtido!
Para conseguir calcular o calor específico a volume constante das três substâncias, precisamos lembrar da única fórmula que temos pra isso. Ela é a derivada parcial da energia interna específica em relação à temperatura , mantendo o volume específico da substância constante.
Para conseguir informações sobre a variação da energia interna específica a volume constante a partir das informações dadas de calor absorvido , temos que utilizar a primeira lei nessas três substâncias (, e ).
O enunciado informa todos os valores de massa.
Ele também diz indiretamente que as substâncias não realizam nem sofrem nenhum trabalho durante o aquecimento. O enunciado faz isso, dizendo que as três substâncias estão em tanques rígidos. Como a parede do tanque não se move, o volume das substâncias não variam. Por causa disso, elas não podem sofrem nem realizar trabalho de movimento de fronteira.
Ou seja, o processo de aquecimento ocorre sem trabalho e a volume constante! A variação de energia interna ocorre a volume constante! Por isso podemos usar os dados do gráfico para utilizar nos cálculos de calor específico a volume constante! Além disso, o gráfico informa o calor absorvido pelas substâncias do ponto 1 até o ponto 2 marcado no gráfico.
Com esses dados, podemos calcular as variações de energia interna específica a volume constante , reorganizando a primeira lei.
Vemos que as variações de energia interna específica dependem da quantidade de calor absorvida . Perceber isso é muito importante, porque a quantidade de calor absorvido varia linearmente. Se a variação de depende de uma quantidade linear , também varia linearmente. Por isso, o calor específico pode ser calculado da seguinte forma.
Vemos pelo gráfico que as temperaturas das substâncias no ponto 1 são iguais a .
Já as temperaturas dos pontos 2 valem:
Com todos esses dados, podemos enfim calcular os calores específicos!
Passo 2
Antes de calcular os calores específicos, temos que calcular a variação de energia interna específica de cada substância.
Com esses valores, podemos encontrar os ’s.
Resposta
A substância