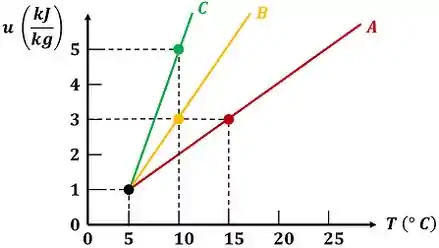
Três substâncias estão contidas cada uma em um tanque rígido. Elas são aquecidas, mantendo seus volumes constantes. O gráfico fornece a variação de energia interna específica de três substâncias , e em função da temperatura, conforme elas recebem calor. Calcule, para cada uma das substâncias, o calor específico a volume constante.
Passo 1
O enunciado quer saber quanto valem os de cada substância, mas ele aparentemente só nos fornece um gráfico da energia interna específica de cada substância em função da temperatura. Qual é a ligação entre os e o gráfico? Será que o gráfico é a única informação que o problema nos dá? Não tem nada escondido no texto do enunciado?

A única forma que conhecemos para se calcular o é através da fórmula abaixo.
Ou seja, ele é a derivada parcial da energia interna específica em relação à temperatura, mantendo o volume específico constante. Isso quer dizer que, para descobrir quanto vale , precisamos saber como varia em função de , enquanto permanece constante!
O gráfico nos mostra como varia em função de , mas será que é constante nesse caso?

Para saber se as substâncias estão ganhando energia, mas mantendo seus volumes específicos constantes, temos que descobrir uma informação que está escondida no texto da questão!
A questão nos diz que as três substâncias estão contidas cada uma em um tanque rígido. Isso significa que os seus volumes (, e ) não variam conforme elas são aquecidas!
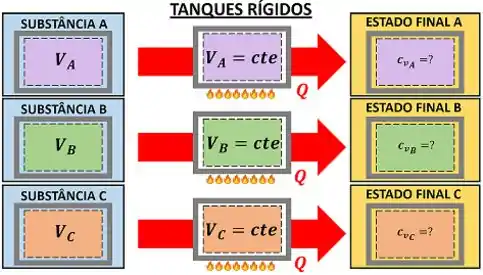
Além disso, as massas (, e ) das substâncias também não variam durante o aquecimento.
O volume específico é igual ao volume dividido pela massa. Como os dois são constantes, o volume específico também é constante no aquecimento do problema!
Isso mostra que a informação presente no gráfico pode ser usada para calcular os , porque é constante durante o aumento de !
E como podemos calcular a derivada parcial com a ajuda do gráfico?
Isso é o que veremos no próximo passo!
Passo 2
A derivada é a inclinação de uma curva em um determinado ponto.
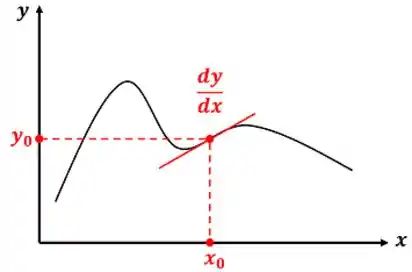
Vemos pelo gráfico que é uma função linear de . Em outras palavras é uma reta. Ou seja, para calcular os três , temos que calcular a inclinação das três retas , e ! A inclinação dessas retas é igual à variação de dividida pela variação de .
Para achar essa inclinação, precisamos de apenas dois pontos da reta. O ponto 1 (ponto com o valor de menor) e o ponto 2 (ponto com o valor de maior).
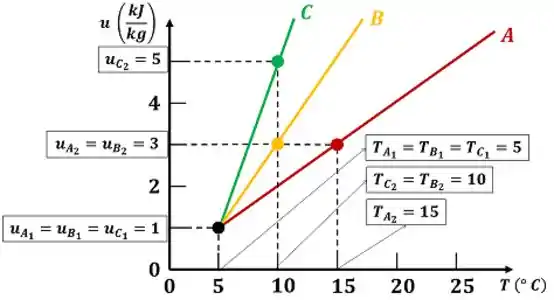
Todas as variáveis necessárias para calcular os são obtidas através do gráfico.
Com esses valores nós podemos começar os cálculos.
Deixaremos essa parte para o próximo passo.