Abaixo é dado uma estrutura com o formato mostrado. Sabendo que a densidade dessa estrutura é de determine o peso próprio dessa estrutura, assim como o seu peso distribuído no comprimento.
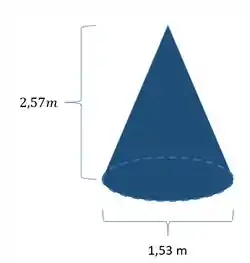
Passo 1
Vamos primeiro descobrir como determinamos o peso próprio dessa estrutura. Para fazermos isso precisamos nos lembrar do passo a passo que vimos na teoria.
Sabemos que o Cálculo do peso é dado pela equação.
Sabemos que m é a massa e g a gravidade. A gravidade já conhecemos o valor, mas e a massa?
Nesse caso temos que lembrar o seguinte
Em que é a nossa densidade e V o volume da nossa peça. O é a nossa densidade, e o volume? Como iremos calcular?
Como a nossa peça é um cone, teremos que a fórmula será
Substituindo na nossa equação teremos que
Para determinarmos o peso próprio distribuído basta dividir o nosso peso próprio pelo comprimento da nossa peça, ou ainda pela altura da nossa peça, fazendo isso teremos que
Vale ressaltar o seguinte, por se tratar de um cone, o raio da peça varia com a altura, logo, o nosso peso próprio distribuído ficará em função do nosso raio, ou ainda da nossa altura, vamos ver as duas respostas, não tendo um valor fixo como o peso próprio que já calculamos.
Passo 2
Agora que já sabemos como fazer o cálculo, vamos determinar o valor de cada um dos nossos termos, dessa forma teremos que
Agora que já temos todos os valores, vamos determinar o peso próprio, substituindo na nossa equação teremos que
E qual a unidade?
Vamos substituir cada unidade na nossa fórmula
Logo nosso peso próprio será
Passo 3
Agora para determinar o peso próprio distribuído precisamos lembrar da nossa fórmula
Já temos quase todos esses valores, só temos que por o raio em função da altura da nossa peça, para isso vamos ver o seguinte esquema
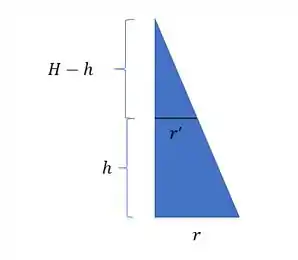
Nosso objetivo é determinar o valor de r’, para isso basta fazer uma regra de 3
Isolando r’ teremos que
Para testar vemos o seguinte, como a nossa origem está embaixo temos que ver que
então
E se
então
E vemos que se fizermos essa comparação com o nosso esquema vai estar tudo correto. Substituindo agora essa equação na nossa fórmula principal teremos que
Como queríamos, a nossa fórmula ficará em função de h, substituindo
Lembre que nesse caso a nossa unidade é