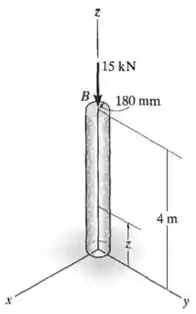
A coluna é feita de concreto de densidade e está sujeita a uma força de compressão axial de em sua extremidade superior . Determine a tensão normal média na coluna em função da distância medida em relação à base.
Passo 1
O que está acontecendo?
A coluna tem um comprimento inicial e uma seção transversal circular de raio .
O exercício diz que a coluna possui uma densidade (mega-gramas por metro cúbico), então ele quer que a gente considere o peso próprio da coluna.
O peso próprio total da coluna é igual a sua massa vezes a gravidade :
Mas a massa da coluna é igual a sua densidade vezes o seu volume , ainda
E o volume da coluna é igual à sua área de seção transversal vezes o seu comprimento :
Beleza...
Mas sabemos que na verdade, o peso da coluna não é uma força pontual , e sim uma carga distribuída uniformemente ao longo de todo o comprimento da coluna.
Chamando essa carga distribuída de , vamos ter que:
Então tá... e o que é que isso significa?
Isso significa que se a gente fizer o diagrama de corpo livre da coluna, vamos ter:
- A força de compressão ;
- Uma força de reação do solo;
- E, também, uma carga distribuída de peso próprio .
Desenhando a carga distribuída de uma outra cor, para que a gente possa diferenciar ela das forças pontuais e , o diagrama fica assim:
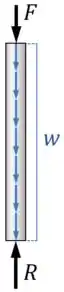
E o que é que o exercício quer?
Ele quer que a gente encontre uma expressão que fornece a tensão normal média dependendo do ponto da coluna que estiver sendo avaliado.
Para calcular essa tensão , vamos precisar da força interna normal , que vamos encontrar através de uma análise dos esforços internos na barra.
Antes de fazer essa análise, temos que aplicar as condições de equilíbrio na barra para que a gente possa descobrir o valor da reação desconhecida.
Observação: Vamos assumir que .
Passo 2
Então vamos começar fazendo um diagrama de corpo livre da coluna:
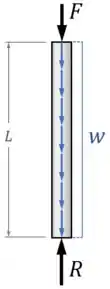
Com isso, podemos aplicar as condições de equilíbrio nela.
Aqui, só vamos ter disponível o equilíbrio de forças na vertical:
Fazendo esse somatório de forças, vamos ter a reação para cima, a força para baixo e a força equivalente à carga distribuída para baixo.
Essa força equivalente vai ser igual à distribuição uniforme vezes o comprimento em que ela atua.
Então o somatório de forças fica assim:
Isolando , encontramos que:
Vamos guardar esse valor para depois!
Passo 3
Agora, para encontrar a força interna normal na coluna, vamos fazer uma análise de esforços internos nela.
Secionando a coluna em uma seção genérica com uma posição , que pode variar entre e , vamos ter o desenho abaixo:
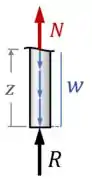
Para determinar , usamos o equilíbrio de forças na vertical:
Nesse caso, temos as forças e para cima e a força equivalente a carga distribuída para baixo.
Como é uniforme e atua ao longo de um comprimento , essa força equivalente vai ser igual à .
Sendo assim, o somatório de forças acima fica assim:
Isolando , encontramos que:
Mas no final do passo anterior guardamos a Equação 1 que diz que , então temos que:
Fazendo a distributiva do sinal de negativo, isso fica assim:
E, finalmente, colocando em evidência, encontramos que:
Passo 4
Encontrada uma expressão para a força normal , já podemos determinar a tensão normal média na coluna:
Substituindo a expressão encontrada para , temos:
Lá no Passo 1, vimos que .
Substituindo isso, temos que:
Realizando a divisão por , isso fica assim:
Como a seção transversal da coluna é circular de raio , a sua área pode ser calculada pela fórmula .
Fazendo essa substituição e fazendo a distributiva na multiplicação , temos:
E, finalmente, arrumando tudo, encontramos que:
Passo 5
Agora, só falta substituir os valores...
- ;
- ;
- ;
- ;
- & ,
- ;
- (!);
- ;
- ;
- & .
...na expressão que acabamos de encontrar para que a gente possa determinar .
Mas antes disso, vamos prestar atenção nas unidades das nossas variáveis:
Primeiro, a força está em e o raio está em , então o termo vai sair em que é o mesmo que .
Além disso, a densidade está em e a gravidade está em .
Dessa forma, os termos vão sair em:
Como é o mesmo que , isso pode ser reescrito assim:
Além disso, é o mesmo que , então essas unidades equivalem à:
E, por fim, é o mesmo que .
Ou seja, os termos vão sair em .
Quando esses termos forem multiplicados por ou por , que são dados em , o resultado de tensão vai sair em . 👈
Então para padronizar tudo, vamos reescrever o raio como .
Com isso, o termo também vai sair em . 👍
Passo 6
Então...
Vamos pegar a expressão que encontramos para a tensão :
E substituir nela os valores:
Fazendo isso e calculando tudo, encontramos que:
Como pode variar entre e , essa tensão sigma vai ser sempre negativa, já que o termo nunca vai ser maior que .
Então podemos arrumar a nossa resposta para deixar claro que essa tensão será negativa (ou seja, que ela será uma tensão de compressão):
E assim terminamos o exercício!