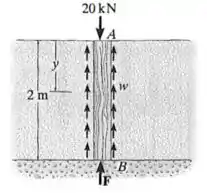
O poste é feito de abeto Douglas () e tem diâmetro de . Se estiver sujeito a uma carga e o solo proporcionar resistência ao atrito que varia linearmente de em a em , determine a força em sua parte inferior necessária para haver equilíbrio.
Calcule também qual é o deslocamento da parte superior do poste, , em relação à sua parte inferior, . Despreze o peso do poste.
Passo 1
O que está acontecendo?
O poste tem um comprimento inicial , uma seção transversal circular de diâmetro e um módulo de elasticidade .
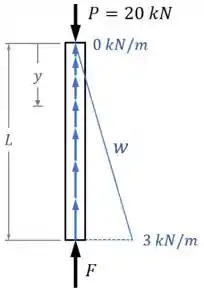
Ele está sob uma carga e é sustentado por uma força em sua parte inferior e pela força de atrito linearmente distribuída , como mostra o seu diagrama de corpo livre:
E o que é que o exercício quer?
Primeiro, ele quer que a gente descubra o valor da força na parte inferior do poste.
Para encontrar , vamos ter que calcular uma força equivalente à carga linearmente distribuída para, em seguida, podemos aplicar o equilíbrio de forças no poste.
Em seguida, ele quer que a gente calcule o deslocamento da parte superior do poste em relação à parte inferior .
Ou seja, ele quer saber a variação de comprimento sofrida pelo poste.
Como temos uma força distribuída, essa variação de comprimento vai ter que ser calculada pela fórmula:
No nosso caso:
- O módulo de elasticidade e a área de seção transversal ;
- E o carregamento no poste, e, consequentemente, a força interna normal no poste, variam em função da coordenada , e não da coordenada .
Dessa forma, a fórmula para vai ficar assim:
Agora, antes de usar essa fórmula, vamos ter que fazer uma análise dos esforços internos no poste para encontrarmos uma expressão para a força normal .
E, antes disso, vamos ter que formular uma expressão para a carga distribuída .
Passo 2
Vamos começar pela primeira parte do exercício: calcular a força .
Para tanto, fazemos um diagrama de corpo livre no poste:
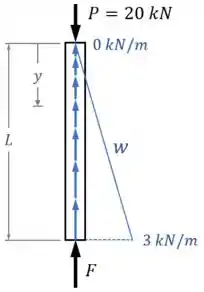
E aplicamos as condições de equilíbrio nele.
Nesse caso, podemos aplicar o equilíbrio de forças na vertical:
Para fazer esse somatório de forças, precisamos definir uma força equivalente à carga distribuída .
O jeito mais fácil de fazer isso é observar que varia linearmente entre e , de tal forma que o seu valor médio é .
Esse valor médio distribuído ao longo do poste de comprimento , vai resultar em uma força resultado .
Sendo assim, o somatório de forças acima fica assim:
Como queremos saber o valor de , vamos isolá-lo:
Substituindo , e , encontramos que:
Passo 3
Agora seguimos para a segunda parte: calcular a variação de comprimento causada no poste pelas cargas que atuam nele.
Antes de usar a fórmula de , temos que formular expressões que para a carga distribuída e para a força normal variável na coluna.
Então vamos pensar...
Sabemos que varia linearmente. Então podemos formular em função de assim:
Agora...
Quando , é igual à , ou seja:
O que significa que:
Por outro lado....
Quando , é igual à , ou seja:
Substituindo e isolando , encontramos que:
Dessa forma, temos que em função de pode ser formulado assim:
Passo 4
Em seguida, para encontrarmos uma fórmula para a força normal variável , precisamos fazer uma análise de esforços internos no poste.
Secionando o poste em uma seção genérica com uma posição , o desenho da análise de esforços internos fica assim:
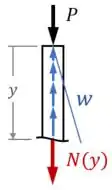
Aplicando o equilíbrio de forças na vertical, vamos ter:
Para fazer esse somatório, precisamos definir uma força equivalente à carga distribuída nesse trecho da peça.
Então vamos pensar...
Nesse trecho, começa igual à e varia linearmente até seu valor máximo no ponto .
Como vimos no passo anterior, no ponto vai ser dado pela fórmula:
Então o valor médio de no trecho que estamos estudando vai ser a metade disso:
Esse valor médio distribuído ao longo de um trecho de comprimento vai resultar em uma força equivalente:
Sabendo disso, conseguimos fazer nosso somatório de forças, que fica assim:
Queremos encontrar a força normal em função de (“”), então devemos isolá-la:
Passo 5
Agora que conhecemos , podemos aplicar a fórmula:
Primeiro, podemos tirar para o lado de fora da integral as constantes e :
Além disso, sabemos que a área da seção transversal circular de diâmetro do poste pode ser dada pela fórmula .
Dessa forma, temos que:
Arrumando tudo, essa expressão fica assim:
Feito isso, vamos focar agora em calcular a integral, que vamos chamar de :
Substituindo a expressão encontrada para , ficamos com a integral de um polinômio:
Então lembra aí!
A integral desse polinômio vai ficar assim:
Fazendo a diferença entre os valores nos extremos, temos:
O segundo termo vai ser nulo, então só vai sobrar:
Substituindo e , vamos encontrar que:
E pronto!
Agora podemos voltar na variação de comprimento :
E substituir o valor da integral:
Substituindo e , as unidades e vão se cortar.
Com isso, nosso resultado para vai sair na unidade que sobra, que é metros ().
Fazendo essas substituições e calculando tudo, encontramos:
Como esse número é muito pequeno, podemos reescrevê-lo em :
E assim terminamos a segunda e última parte do exercício.