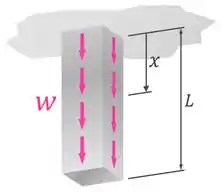
A barra de aço () da figura abaixo possui uma seção transversal uniforme de área e um comprimento original .
O peso próprio do aço gera na barra uma carga axial uniformemente distribuída . Essa carga, por sua vez, gera na barra uma força normal descrita pela fórmula .
Determine a variação de comprimento causada nessa barra por esse carregamento de peso próprio .
Passo 1
O que está acontecendo?
O carregamento na barra de aço devido ao seu peso próprio gera nela uma força interna normal que varia em função do ponto que está sendo avaliado na barra:
Onde é o carregamento distribuído na barra e é o comprimento inicial da barra.
A barra ainda tem um módulo de elasticidade e uma área de seção transversal .
E o que é que o exercício quer?
Ele quer saber qual é a variação de comprimento causada pelo carregamento na barra.
A gente sabe que essa variação de comprimento é normalmente dada pela fórmula:
Mas a força normal na nossa barra varia ao longo do comprimento da barra.
Então vamos ter que recorrer à fórmula:
Como no nosso caso, o módulo de elasticidade e a área de seção transversal da barra são constantes, essa fórmula vai ficar assim:
Substituindo os valores de , , e nessa fórmula, vamos conseguir calcular !
Passo 2
Para que a gente já possa calcular e se livrar da integral, vamos começar substituindo .
Fazendo essa substituição na fórmula, temos:
Podemos colocar o termo constante que multiplica toda a expressão do lado de fora da integral.
Fazendo isso, temos:
Agora temos que nos lembrar de como se faz uma integral. 😖
Lembra aí...
Para fazer a integral de um polinômio, a gente dá um expoente para em cada termo, aumenta em cada expoente e divide cada termo pelo novo expoente:
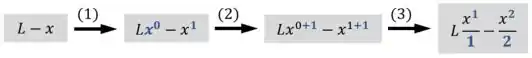
Então a nossa integral vai ficar assim:
O que significa que:
O primeiro termo vai dar enquanto que o segundo vai dar , então:
Com isso, a nossa expressão para fica assim:
Finalmente, substituindo os valores de , , e , vamos ter que:
Reescrevendo como e expandindo o , temos:
Cortando com , com e com , vemos que o nosso resultado vai sair em metros:
Calculando tudo, encontramos:
Como esse número é bem pequeno, podemos reescrevê-lo em na hora de dar a resposta: