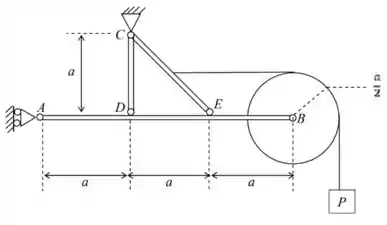
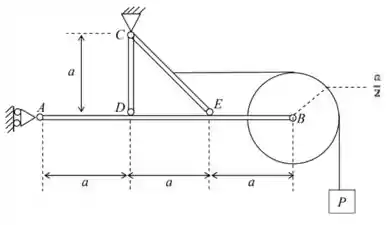
03) A estrutura plana ilustrada na figura é constituída pelas barras articuladas e , de peso desprezível. Em há uma polia de peso desprezível que sustenta uma carga de peso por meio de um cabo inextensível e de peso desprezível. Pede-se:
a) desenhar o diagrama de corpo livre do conjunto;
b) determinar as reações em e em
c) desenhar o diagrama de corpo livre da polia;
c) desenhar os diagramas de corpo livre das barras e ;
d) determinar as forças internas atuantes nas barras , e .
Passo 1
Faaaaaala gente bonita, como vocês estão?
Nessa questão temos um conjunto de barras, ligadas a dois apoios, com uma polia articulada na extremidade de uma das barras. Por essa polia, passa-se um fio que sustenta uma carga . Temos uma situação de equilíbrio estático, então já vai buscando na memória as equações desse tipo de equilíbrio 😊

a) Pra começar, devemos desenhar o diagrama de corpo livre (DCL) do conjunto. Esse é um detalhe importante, como queremos o DCL do conjunto, não vamos nos importar com as forças internas entre as barras, ou com a reação na articulação da polia, queremos apenas as forças externas ao nosso sistema. Beleza?

Vamos identificar as forças externas agindo no nosso conjunto.
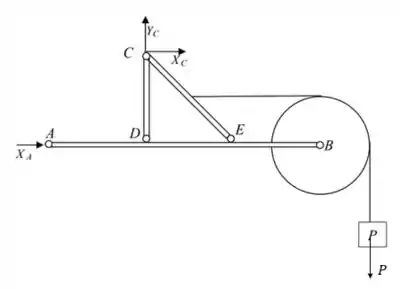
Devido ao apoio em ser do gênero, teremos apenas a reação no eixo da barra . Já em , temos um apoio do gênero, que nos dará reação nos eixos vertical e horizontal. Fora isso, temos também a força peso atuando na carga . Daí, podemos desenhar o seguinte DCL:
Passo 2
b) Devemos agora determinar as reações em e em .
Lembra do que falamos no início? Quais equações decorrem do fato de termos um equilíbrio estático?
Sempre que temos equilíbrio estático, podemos escrever duas equações:
No caso, o momento em relação a qualquer ponto é nulo.
Aplicando a equação da força resultante nula, vamos ter que: 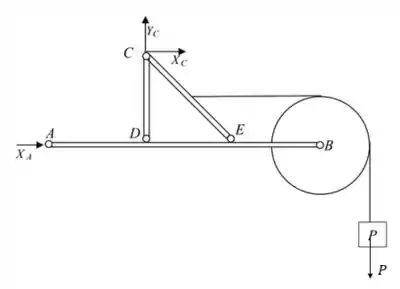
Usando a equação do momento em relação ao ponto (pois é o ponto onde atuam mais forças), vem:
Logo:
E, pela primeira equação:
Prontinho 😉
Passo 3
c) Devemos desenhar o DCL da polia.
Nela, atuam a força de tração em duas direções diferentes, uma no eixo horizontal, e outra no eixo vertical. Além disso, a articulação em também provoca reação nos dois eixos. Daí:
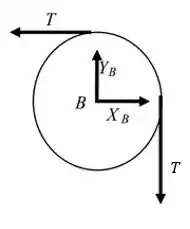
Legal perceber que, devido à carga presa no fio, temos .
Além disso, como a polia está em equilíbrio, devemos ter:
Passo 4
d) Agora devemos desenhar o DCL das barras e . A diferença em relação ao item a) é que queremos o diagrama de cada barra, então a nossa ideia de “força externa” muda um pouco.
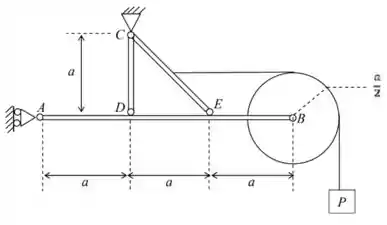
Para a barra , por exemplo, temos a reação no apoio em igual tinha antes. Mas, temos também a reação da articulação da polia na barra, que deve ser uma força no eixo vertical e outra horizontal. Além disso, também há a força normal de contato das barras e , em e em ( Lembrando que em teremos uma reação nos dois eixos). Logo:
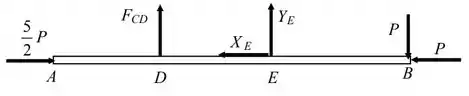
Na barra é um pouco mais simples, temos apenas uma força tracionando-a ao longo do seu eixo.

Por último, na barra , temos as reações do contato de em (no sentido oposto ao desenhado no DCL de ), além das reações verticais e horizontais da articulação em . Fora isso, o fio também está preso nessa barra, puxando-a com .
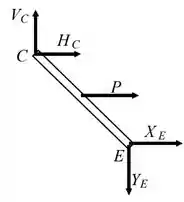
Passo 5
e) Por último, devemos determinar as forças internas às barras e . Ou seja, são justamente as forças que desenhamos no DCL das barras no item anterior.
Novamente, como tudo está em equilíbrio estático, para a barra podemos escrever que:
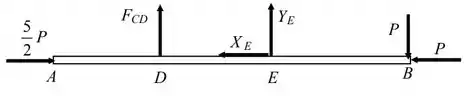
Equilíbrio de forças na horizontal:
Equilíbrio de forças na vertical:
Momento nulo em relação a :
Logo:
Bouaaa! Olhando agora para o equilíbrio da barra , temos:
Equilíbrio na vertical:
Equilíbrio na horizontal:
Substituindo o valor de :
Prontinho!! Com isso determinamos todas as forças internas às barras!
Conseguiram entender bem? É isso galera, tamo junto! Até a próxima ;)
Resposta
Resolução no texto.