Uma peça foi sujeita ao carregamento distribuído abaixo. Sabendo que ela sofrerá uma carga como mostrado na figura, determine a deformação total que ela sofrerá.
Dados do problema.
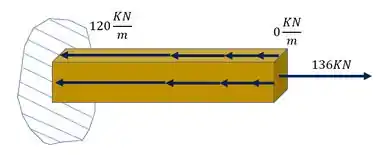
Passo 1
Para podermos determinar qual a deformação total da nossa peça, precisamos saber como calcular essa deformação. Para esse tipo de caso a fórmula é dada por
Sabemos que o valor da área podemos determinar facilmente pelos dados do enunciado, tendo dessa forma que
E o modulo de elasticidade é
Agora para podermos continuar as contas precisamos determinar a equação do nosso normal
Passo 2
Para determinarmos o normal precisamos dividir a nossa peça e analisar como o nosso normal é determinado pelo equilíbrio da peça. A nossa origem será definida na extremidade da barra com carregamento concentrado. E o sentido será da direita para esquerda. Analisando a nossa peça cortada teremos que
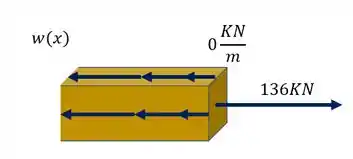
Usualmente arbitramos o nosso normal saindo da peça, e como a nossa origem está na direita, iremos colocar que a distância em que fizemos o corte é X.
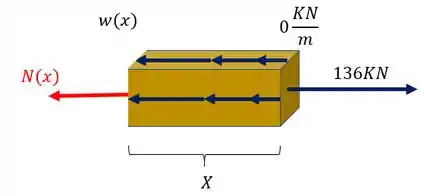
Passo 3
Antes de começarmos a fazer o equilíbrio precisamos fazer uma troca, ou seja, devemos trocar a nossa carga distribuída por uma carga concentrada, mas como faremos isso?
Você tem que pegar o seguinte macete, para trocarmos uma carga distribuída por uma concentrada precisamos calcular uma área, mas que área é essa?
Precisamos visualizar ela na nossa peça
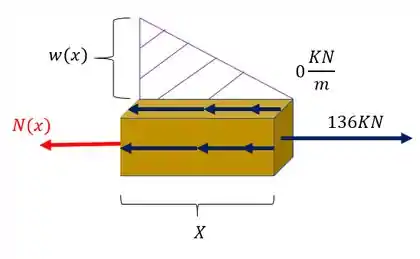
Esse triangulo representa como a carga distribuída se comporta na nossa peça, ela começa no zero e vai aumentando linearmente até o valor . Se calcularmos a área desse triangulo, determinamos o valor da carga concentrada que entraria no lugar dessa carga distribuída. Porém para calcularmos essa área necessitamos do valor de . Como ele cresce linearmente com o valor de X, podemos determinar uma equação do primeiro grau para o nosso triângulo, usando as condições de contorno do nosso problema, ou seja, os valores que temos nas extremidades.
Passo 4
Vamos calcular o valor de olhando a figura total teremos o seguinte triangulo
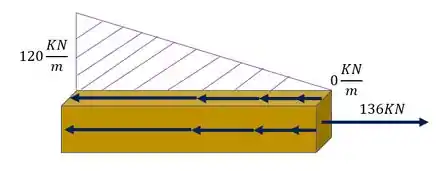
Como queremos montar uma equação da reta usaremos a equação
Precisamos agora resolver o seguinte sistema
E
Substituindo a primeira equação teremos que
Logo
Já com o valor de b vamos substituir o próximo valor que será
Logo
Jogo a nossa equação da reta será
Como o nosso objetivo era determinar a equação da carga distribuída podemos definir que
Passo 5
Voltando na nossa figura anterior, agora podemos calcular a área do nosso triangulo
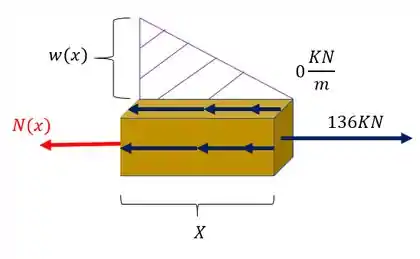
Substituindo a nossa carga distribuída pela concentrada podemos visualizar o nosso desenho como
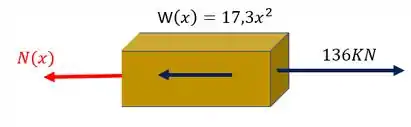
Agora sim podemos fazer o equilíbrio de forças e determinar o valor do nosso normal
Fazendo
Teremos que
Como já determinamos a nossa carga concentrada teremos que
Uma forma de saber se fizemos o cálculo certo é calcular o normal na base da nossa peça e comparar com a área do triangulo grande, fazendo primeiro a área teremos que
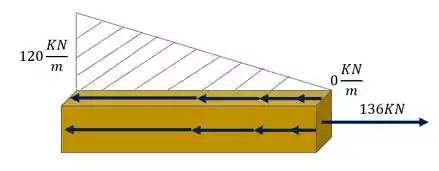
Como tem uma carga de 136 concentrada, também precisamos contabilizar ela para o cálculo do nosso normal na base, logo teremos que
Usando a fórmula do nosso normal com x=3,47 teremos que
Lembrando que o sinal do normal é negativo pois indica compressão. Como em módulo os valores são iguais, então podemos ficar tranquilos que de fato a nossa fórmula está correta. Logo a equação do normal é
Passo 6
Como já temos a equação do normal, podemos substituir todos os valores da nossa integral e em fim calcular a deformação total da nossa peça, substituindo teremos que
Resolvendo teremos que
Substituindo teremos que