Determine o alongamento da tira de alumínio quando submetida a uma força axial de . .
Passo 1
O que está acontecendo?
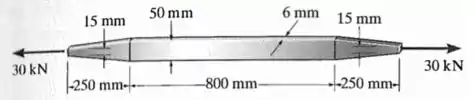
A tira de alumínio é composta por três segmentos e possui um módulo de elasticidade .
Um segmento, central, possui uma área de seção transversal e um comprimento inicial .
Os outros dois segmentos, laterais, possuem um comprimento inicial e uma área de seção transversal variável :
Além de tudo isso, por causa da força axial de tração de , vai haver ao longo de toda essa tira de alumínio uma força interna normal constante .
E o que é que o exercício quer?
Ele quer saber o alongamento, ou seja, a variação de comprimento da tira de alumínio devido à carga aplicada de .
Essa variação de comprimento da tira vai ser a soma das variações de comprimento do segmento central e dos segmentos laterais:
E como é que a gente pode calcular essas variações de comprimento?
Para o trecho central que possui uma área de seção transversal constante, vamos calcular a sua variação de comprimento usando a fórmula .
Já para os dois trechos laterais, a área de seção transversal varia. Então vamos ter que usar a fórmula:
No caso dos nossos trechos laterais:
- A força interna normal e o módulo de elasticidade são constantes;
- A área de seção transversal é chamada de ;
- E o comprimento é chamado de .
Então essa fórmula fica assim:
Agora, antes de usarmos essa fórmula, precisamos formular uma expressão para a área variável .
Passo 2
Então vamos começar o exercício tentando formular uma expressão para .
Se formos observar a geometria dos segmentos laterais, vamos ver que eles têm:
- Uma largura fixa ;
- E uma altura que varia linearmente de no ponto inicial à no ponto final.
A figura abaixo mostra isso visualmente:
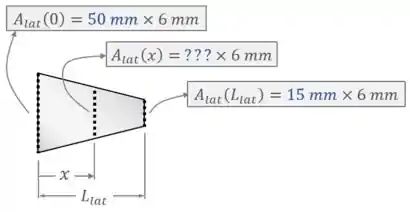
Então vamos chamar essa altura variável de .
Se ela varia linearmente em função de , então ela pode ser expressa pela fórmula:
Por um lado, sabemos que quando , essa altura é igual à .
Ou seja:
Assim, descobrimos que:
Por outro lado, sabemos que quando , a altura é igual à .
Ou seja:
Substituindo e isolando , encontramos que:
O que significa que:
Substituindo , encontramos que:
Sendo assim, podemos descrever a altura assim:
Sabendo que e que !
Agora, a área de uma seção transversal dos segmentos laterais da tira é a multiplicação dessa altura variável pela largura da peça.
Então pode ser descrita em função de assim:
Passo 3
Agora que temos uma fórmula para em função de , já podemos calcular a variação de comprimento nos segmentos laterais da tira:
Primeiro, substituímos a expressão encontrada para :
Em seguida, podemos tirar as constantes , e para o lado de fora da integral:
Com isso, vamos focar na resolução da integral, que vamos chamar de :
É, olhando para essa integral já dá para ver que ela não é tão fácil...

Mas vamos lá, você aguenta:

Faz tempo que eu não vejo cálculo, mas o meu instinto é de fazer uma substituição.
Então vamos tentar isso.
Vamos dizer que .
Derivando em relação a , vamos ter que:
O que significa que:
Beleza, então vamos olhar para o que está dentro da nossa integral:
Substituindo , fica assim:
Depois, multiplicamos em cima e em baixo por :
Com isso, podemos substituir :
Agora, podemos atualizar a nossa integral com essa substituição, tendo o cuidado de também atualizar os intervalos da integral:
Arrumando tudo e colocando a constante para fora, a nossa integral fica assim:
E olha só, integral de a gente sabe que dá , então temos que:
Fazendo a diferença entre os valores nos extremos, temos:
Mas lembra aí!
Existe uma propriedade dos logaritmos que diz que .
Aplicando essa propriedade, o resultado da nossa integral fica assim:
E pronto, está resolvida a integral!

Beleza, então vamos voltar na expressão que tínhamos encontrado para :
E substituir o valor que encontramos para a integral:
Substituindo nessa expressão:
- ;
- ;
- ;
- ;
- ;
- & ,
Vamos encontrar que:
Passo 4
Encontramos o valor de , então agora só falta encontrar o valor da variação de comprimento do segmento central da tira, que é muito mais fácil de calcular.
Nesse segmento central nós temos um comprimento , além de uma força normal , um módulo de elasticidade e uma área de seção transversal constantes.
Sendo assim, a variação de comprimento vai ser dada pela fórmula:
Substituindo , , e , vamos encontrar que:
Passo 5
Finalmente, podemos somar as variações de comprimento dos diferentes segmentos da tira de alumínio para encontrar a variação de comprimento total da tira:
Substituindo os valores de e , encontramos que:
O que dá a nossa resposta: