Calcular o rendimento térmico e o título na saída do ciclo Rankine, que opera entre 4 MPa e 7,5kPa, com superaquecimento de 250°C.
Passo 1
A diferença básica entre os dois ciclos é que no sem superaquecimento o vapor entra como vapor saturado na turbina, ou seja, esse ponto está exatamente sobre o “sino”. Já no ciclo com superaquecimento o vapor entra na turbina como vapor superaquecido, ou seja, este ponto está acima do “sino”. O desenho abaixo mostra o diagrama com superaquecimento.
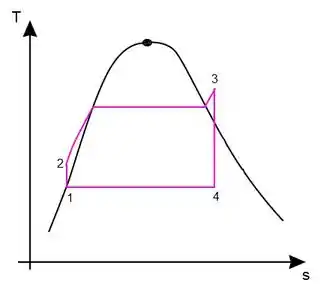
Para resolver esse problema vamos ter que dar uma olhada nas tabelas de saturação e de vapor superaquecido da água, assim, vamos achar o título e as entalpias de cada estado termodinâmico e, finalmente, calcular a eficiência.
Passo 2
A eficiência é dada por
O trabalho da bomba é um trabalho de fluxo, ou seja, há variação da pressão enquanto o volume específico se mantém constante, portanto é definido como
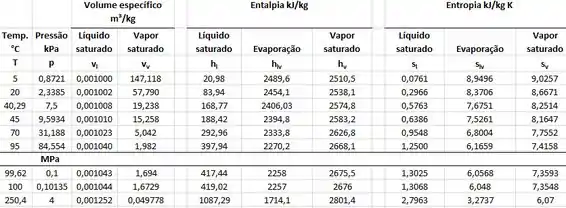
Pela tabela de saturação, o líquido saturado a pressão de 7,5 kPa tem
Então o trabalho consumido na bomba é de
Passo 3
Como o trabalho também pode ser calculado como a diferença de entalpias, e pela tabela a entalpia de um líquido saturado a pressão de 7,5 kPa é , então
Observe que o sinal negativo foi colocado porque a bomba recebe trabalho, ao invés de gerar.
Agora já temos a entalpia dos estados 1 e 2, vamos calcular a do estado 3.
Passo 4
O estado 3 é um estado de vapor superaquecido com pressão de 4 MPa. Como sabemos a pressão, temos de saber também a temperatura, como o enunciado nos forneceu que o superaquecimento é de 250°C então
Esse 250,40 que somamos é a temperatura de saturação na pressão de 4Mpa. Por isso que T3 vai ser soma da temperatura de saturação com a temperatura de aquecimento.
Com os dados fornecidos neste estado temos:
Passo 5
Agora vamos descobrir a entalpia do estado 4. Neste estado estaremos trabalhando novamente com a pressão de 7,5 kPa e temperatura de 40,29°C mas presta atenção, aqui temos uma mistura de líquido e vapor, então esse estado é diferente do 1.
Com isso precisamos saber o título deste estado, que achamos por meio da entropia. Como o processo 3 – 4 é isentrópico, então a entropia de 4 é igual a de 3.
Fazendo um processo semelhante para achar a entalpia
Passo 6
Agora podemos achar o rendimento para o ciclo sem superaquecimento
Como podemos colocar todos esses valores com diferenças de entalpias, temos