Uma central de potência a vapor, operando num ciclo de Rankine, apresenta pressão máxima igual a 5 MPa e mínima de 15 kPa. Sabendo que o valor mínimo aceitável para o título do vapor na seção de saída da turbina é de 95% e que a potência gerada na turbina é igual a 7,5MW, determine qual é a temperatura de descarga da caldeira e a vazão em massa no ciclo.
Dado: Para o vapor superaquecido a 700°C têm-se uma entropia igual a 7,5122 e para a temperatura de 800°C a entropia é igual a 7,7440.
Passo 1
Para começar esse problema, e qualquer outro desse tópico, temos de achar as propriedades de algum estado termodinâmico. Lembrando que um estado termodinâmico é definido por duas propriedades independentes (como a pressão e a temperaura) e, se for o caso de uma mistura de fases, o título também deve ser considerado já que na mudança de fase a pressão e temperatura são dependentes.
O meio mais fácil de achar esse estado é a saída da turbina que é onde ocorre a pressão mínima de 15 kPa e o título de 95%, essas duas propriedades já bastam e o estado está definido. Vamos ter apenas que olhar na tabela e fazer aquelas operações para achar outras propriedades importantes como a entropia e a entalpia.
Passo 2
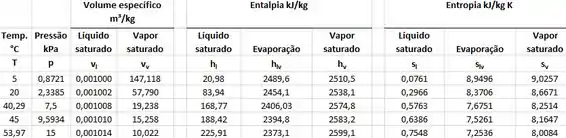
Calculando a entalpia e entropia do estado 4 (saída da turbina). Ao olhar a tabela da água saturada a 15 kPa encontramos que
Como sabemos que o título é igual a 95% podemos calcular a entalpia e a entropia desse estado da forma:
Passo 3
Agora vamos achar a temperatura de descarga da caldeira, que é a mesma de entrada na turbina. Vamos fazer isso lembrando que o processo na turbina é isentrópico ou seja , como sabemos também que a pressão é de 5 MPa basta ir novamente na tabela. Quando olhamos na tabela de vapor d’água superaquecido, na parte referente à pressão de 5 MPa, vemos que essa entropia de não é encontrada diretamente, porém, está entre os valores de 7,5122 e 7,7440 que representam, respectivamente, as temperaturas 700°C e 800°C.
Então agora é só fazer uma interpolação linear (aquela lá de quando estudamos transformação de celsius para fahrenheit) para achar a temperatura aproximada:
Passo 4
Agora vamos achar a vazão mássica, faremos isso por meio da potência da turbina que foi dada na questão:
Agora nos deparamos com uma situação parecida com a do passo anterior, pois sabemos o estado 3 mas a tabela não fornece o valor exato. Então, vamos ter que fazer novamente uma interpolação.