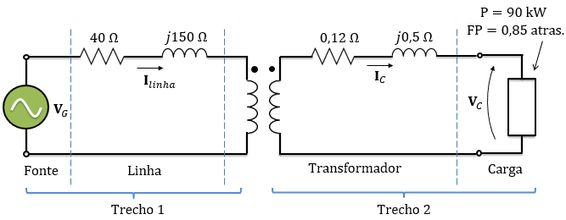
Considere o circuito abaixo. A fonte alimenta um transformador através de uma linha de transmissão. A impedância série do circuito equivalente do transformador referida ao lado de menor tensão é . A carga que está conectada ao transformador é de com fator de potência igual a atrasado, e a tensão entre seus terminais é igual a . Pergunta-se:
Qual a tensão da fonte (fasor)?
Qual é a regulação de tensão do transformador?
Qual é a eficiência total desse sistema?
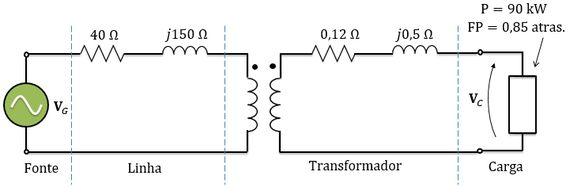
Passo 1
Já fizemos um exercício muito parecido com esse, mas, agora, vamos resolver esse exercício de uma outra maneira. Vamos resolvê-lo utilizando sistema PU.
Então, como vamos trabalhar em pu, temos que encontrar o valor base das grandezas. Podemos dividir esse sistema em dois trechos. O trecho que é o lado do primário do transformador e o trecho que corresponde ao lado do secundário.
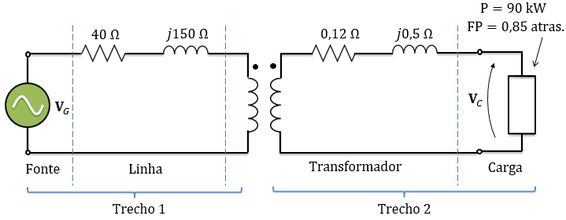
Passo 2
Vamos escolher como bases os valores nominais do transformador. Logo a potência base escolhida para todo o sistema será:
Além disso, cada trecho vai ter uma tensão base:
Com esses valores bases a gente já consegue determinar os valores base para a impedância e corrente das duas regiões.
Passo 3
Agora que os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
Da trecho 1, calculamos a impedância por unidade da linha:
Já do trecho 2, calculamos a impedância série do circuito equivalente do transformador em pu:
Além disso, vamos considerar que a tensão da carga está na referência, ou seja, seu ângulo é zero:
Como o transformador alimenta uma carga com e atrasado, podemos encontrar o conjugado da corrente na carga.
Como,
E
Além disso, o ângulo da potência complexa é o ângulo do fator de potência. Como o fator de potência é atrasado, a carga é predominantemente indutiva e seu ângulo é positivo.
Então, calculando a corrente da carga:
Então, passando a tensão e a corrente da carga para pu:
Passo 4
Agora, vamos desenhar o circuito equivalente por unidade desse sistema.
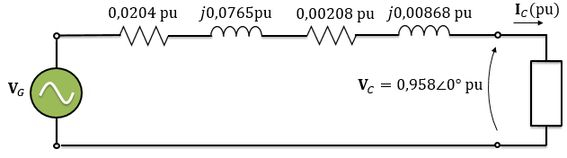
Agora é aplicar a lei das tensões de Kirchhoff na malha do circuito:
Encontramos a tensão do gerador em pu. Agora, precisamos passá-la para volts. Para isso, temos que multiplicar o valor em pu pelo valor base da tensão do gerador.
Como o gerador está no primeiro trecho, sua tensão base é . Logo,
Passo 5
Na letra , temos que tomar cuidado, pois temos que calcular a regulação de tensão do transformador e não a regulação de tensão do sistema (linha + transformador).
Então, como queremos calcular a regulação de tensão apenas do transformador, temos que considerar a tensão após a queda de tensão na impedância da linha. Se liga no circuito abaixo:
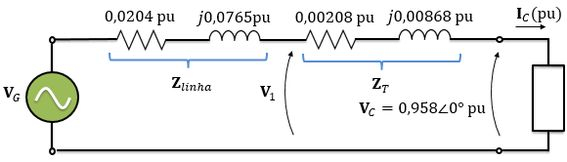
Então, a tensão do primário, em pu, será:
A regulação de tensão é calculada pela seguinte fórmula:
No nosso circuito, quando a carga está ligada, a tensão nos terminais do secundário é igual à tensão que está sendo aplicada na carga. Logo,
Já a tensão a vazio, é a tensão quando retiramos a carga, ou seja, não há corrente e, consequentemente, não tem queda de tensão na impedância equivalente do transformador. Logo, consideremos que toda a tensão do primário é aplicada no secundário.
Então, a regulação de tensão desse transformador será:
Passo 6
O rendimento de um sistema é definido como sendo
Em que a potência de entrada é a soma da potência de saída somado com as perdas na linha de transmissão e no enrolamento do transformador.
Da mesma forma que a regulação de tensão, se queremos calcular o rendimento do sistema, devemos considerar a perda de todos os elementos do sistema (linha de transmissão + transformador).
Nosso sistema é esse:
A potência de saída é a potência ativa na carga, ou seja,
Já as perdas estão relacionadas às resistências da linha e do transformador. Logo,
Então, precisamos calcular em ampéres. Como esta corrente está no trecho 1, temos:
Logo, nossas perdas serão:
Então, a potência de entrada ser��:
Finalmente, o rendimento do sistema será: