Um compressor consome de energia para comprimir de ar. O ar entra na seção de alimentação do compressor a uma temperatura de . Considerando que a vazão volumétrica de ar na seção de descarga do compressor vale , determine a termperatura e a pressão do ar na seção de descarga do compressor. Suponha que o ar escoa em regime permanente através do compressor.
Passo 1
O exercício pede para a gente calcular a temperatura e a pressão do ar saindo do compressor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
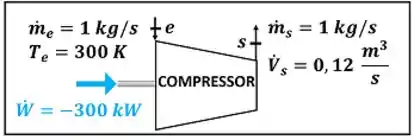
e são as vazões mássicas do ar entrando e saindo do compressor respectivamente. é a vazão volumétrica de ar na saída do compressor. é a temperatura do ar entrando no compressor. é a potência que o compressor consome para funcionar. Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa!

Ela é negativa, porque o compressor está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
Agora que sabemos o que os dados significam, vamos aprender a calcular e nos dois próximos passos
Passo 2
é calculado a partir da primeira lei usada em um compressor em regime permanente. Porém, antes de calcular , precisamos calcular a diferença de entalpia .
Como e , nós podemos colocar qualquer uma dessas vazões em evidência.
A diferença de entalpia do ar possui uma fórmula em função do calor específico a pressão constante do ar.
Substituindo essa fórmula na primeira lei, encontramos uma fórmula para .
será encontrado no passo seguinte!
Passo 3
Para encontar , precisamos calcular o volume específico do ar na saída do compressor primeiro. O valor dessa propriedade pode ser achado por meio da relação entre vazão volumétrica e vazão mássica . A vazão mássica é igual à vazão volumétrica multiplicada pela massa específica do ar saindo do compressor .
Com isso, podemos calcular a pressão através da fórmula de gases perfeitos.
onde é a constante de gás do ar que vale .
Substituindo a fórmula de na fórmula de , achamos:
Tendo toda essa informação em mãos, vamos iniciar as contas no próximo passo!
Passo 4
O valor de do ar em que vamos usar na primeira lei vale:
Substituindo esse valor na fórmula, encontramos:
O valor de é calculado abaixo.