Um compressor, refrigerado a água, é alimentado com R-134a a e . O fluido é descarregado do equipamento a e . Sabendo que a taxa de transferência de calor para a água é e que a potência utilizada para acionar o equipamento é , determine a vazão em massa de R-134a no compressor.
Passo 1
O exercício pede para a gente calcular a vazão mássica que passa pelo compressor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
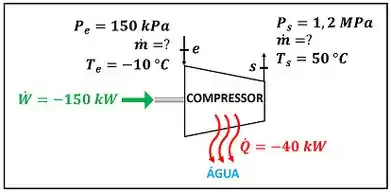
é a vazão mássica de R-134a entrando e saindo do compressor. e são as temperaturas de R-134a entrando e saindo do compressor respectivamente. e são as temperaturas de R-134a entrando e saindo do compressor respectivamente. é a taxa de calor que o compressor perde para a água. é a potência que o compressor consome para funcionar.

Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa!
Ela é negativa, porque o compressor está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
O mesmo acontece com a taxa troca de calor ! A convenção de sinais diz que, quando o equipamento perde calor, é negativo!
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em um compressor em regime permanente. Mas cuidado! O enunciado nos informa a taxa de troca de calor entre o R-134a e a água. Isso significa que a forma da primeira lei que precisamos usar tem que levar em conta o termo de taxa de troca de calor !
Para calcular , precisamos encontrar os valores das entalpias específicas do R-134a entrando no compressor e do R-134a saindo do compressor . Nós vamos aprender a fazer isso no próximo passo!
Passo 3
O R-134a entrando no compressor é um vapor superaquecido porque a sua pressão de é menor que a pressão de saturação dessa substância a . Por isso, temos que procurar o valor da entalpia específica na tabela de vapor superaquecido de R-134a. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
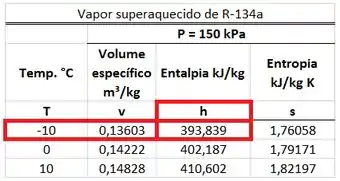
O R-134a saindo do compressor é um vapor superaquecido porque a sua pressão de é menor que a pressão de saturação dessa substância a . Por isso, temos que procurar o valor da entalpia específica na tabela de vapor superaquecido de R-134a. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
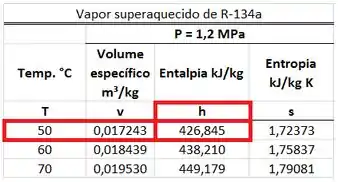
Com esses valores, podemos iniciar as contas!