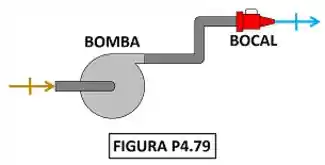
Considere uma bomba hidráulica acoplada a um bocal por meio de uma tubulação curta. Os diâmetros das tubulações de alimentação e descarga da bomba são iguais. O diâmetro de descarga do bocal é igual a . A bomba é acionada por um motor de e é alimentada com água a e . O bocal descarrega o fluido na atmosfera a (veja Figura P4.79). Despreze a energia cinética da água no tubo e considere constante a energia interna da água. Determine a vazão mássica de água e a velocidade de descarga.
Passo 1
O exercício pede para a gente calcular a vazão mássica de água que passa pela bomba e pelo bocal e a velocidade da água saindo do bocal. A diferença desse exercício para um exercício mais simples de bomba é que nesse a gente não analisa só a bomba. Nessa questão a gente vai estudar a bomba junto com o bocal que faz a velocidade água aumentar na saída! A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
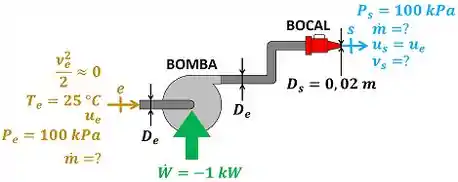
é a vazão mássica de água entrando e saindo da bomba e do bocal. é a temperatura da água entrando na bomba. é a pressão da água entrando na bomba e é a pressão da água saindo do bocal. é a velocidade da água entrando na bomba e é a velocidade da água saindo do bocal. é o diâmetro das duas tubulações que se conectam à bomba. é o diâmetro da saída do bocal. é a energia interna específica da água entrando na bomba. é a energia interna da água saindo do bocal. é a potência que a bomba consome para funcionar.

Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa!
Ela é negativa, porque a bomba está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
Agora que sabemos o que os dados significam, vamos aprender a calcular e .
Passo 2
A velocidade é calculada primeiro. O valor dela é encontrado através da primeira lei e da equação vazão mássica. A forma da primeira lei é a primeira lei para bomba incluindo a energia cinética. No entanto, o enunciado nos informa que a energia cinética da água no tubo deve ser desprezada. Isso significa que o termo de energia cinética da água entrando na bomba pelo tubo deve ser considerado nulo.

Mas CUIDADO! O termo de energia cinética da água saindo da bomba não é nulo, porque a velocidade da água saindo do bocal precisa ser calculada! E Atenção Precisamos dividir essa energia cinética por mil para passar a unidade desse termo de para .
O problema dessa fórmula acima é que ainda não conhecemos , nem para calcular . No próximo passo, nós vamos trabalhar em cima dos termos e !
Passo 3
Nós podemos substituir a fórmula das entalpias específicas e em função das energias internas específicas e na primeira lei.
Mas o enunciado diz que é igual a e que é igual a . Logo:
Nós ainda não conhecemos a variação de volume espeífico para conseguir calcular . Por causa disso, nós vamos olhar esse termo mais a fundo no próximo passo!
Passo 4
A água entra na bomba com e a . Logo, ele entra como um liquido comprimido. O líquido compressível quase não varia seu volume específico, quando é bombeado. Por isso:
Por fim, para achar , precisamos achar uma fórmula para a vazão mássica em função da mássica específica da água líquida comprimida a , da velocidade de saída da água e do diâmetro de saída do bocal .
Atenção! Nas questões de termodinâmica, a massa específica da água líquida comprimida a temperatura ambiente geralmente vale:
Substituindo a equação de na primeira lei, nós criamos uma fórmula para .
Sabendo de tudo isso, podemos iniciar as contas.
Passo 5
Além disso, podemos calcular .