Um dispositivo que opera em regime permanente é alimentado com de amônia a e . A amônia é descarregada do dispositivo a e . As variações de energia cinética e potencial do escoamento de amônia são desprezíveis e o processo realizado no dispositivo pode ser considerado como politrópico. Sabendo que o trabalho específico necessário para acionar um dispositivo é dado por , determine: o expoente politrópico e o trabalho específico e a transferência de calor específica deste processo.
Passo 1
O exercício pede para a gente calcular primeiro o expoente politrópico e depois o trabalho específico e o calor específico . Esse dispositivo recebe trabalho assim como uma bomba e um compressor. Por isso, resolveremos essa questão de forma parecida com as soluções de questões desse equipamento. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
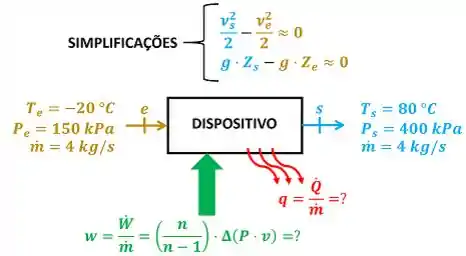
é a vazão mássica de amônia entrando e saindo do dispositivo e do dispositivo. é a temperatura da amônia entrando no dispositivo. é a pressão da amônia entrando no dispositivo e é a pressão da amônia saindo do dispositivo. é a velocidade da amônia entrando no dispositivo e é a velocidade da amônia saindo do dispositivo. é a altitude em relação ao solo da amônia entrando no dispositivo. é a altitude em relação ao solo da amônia saindo do dispositivo. é a potência que o dispositivo consome para funcionar. é a taxa de troca de calor entre o dispositivo e o ambiente. é o trabalho específico que o enunciado pede. é a troca de calor específica que o enunciado pede.

Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
O expoente politrópico é calculado através da fórmula de processos politrópicos mostrada abaixo.
Essa equação nos diz que o termo se mantém constante durante todo o processo que ocorre dentro do dispositivo. Ou seja, da amônia entrando no dispositivo é igual ao da amônia saindo do dispositivo.
onde e são os volumes específicos da amônia entrando no dispositivo e saindo do dispositivo respectivamente!
Reorganizando essa equação, podemos encontrar uma fórmula para .
A fórmula acima mostra que para calcular , temos que encontrar os valores de e . Faremos isso no próximo passo!
Passo 3
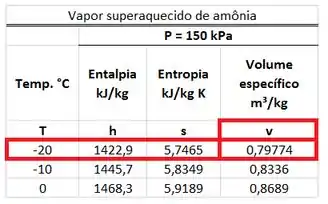
A amônia entrando no dispositivo é um vapor superaquecido porque a sua pressão de é menor que a pressão de saturação dessa substância a . Por isso, temos que procurar o valor do volume específico na tabela de vapor superaquecido da amônia. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
A amônia saindo do dispositivo é um vapor superaquecido porque a sua pressão de é menor que a pressão de saturação dessa substância a . Por isso, temos que procurar o valor do volume específico na tabela de vapor superaquecido da amônia. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
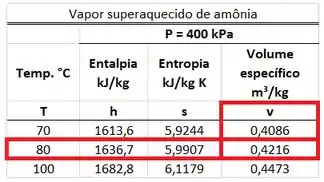
Agor que sabemos quanto valem e , podemos inciar as contas para achar .
Passo 4
Passo 5
Para encontrar o trabalho específico temos que usar a fórmula que o enunciado nos mostrou.
No entanto, é igual a:
Cuidado! Essa fórmula não calcula o trabalho específico com o sinal. O sinal nós teremos que colocar depois! Ele é negativo, porque o dispositivo sofre trabalho!
Com o valor de em mãos, podemos aprender a calcular a troca de calor específica no próximo passo.
Passo 6
A incógnita pode ser calculada através da primeira lei da termodinâmica aplicada ao dispositivo. Lembre-se que o enunciado avisa que as variações de energia cinética e potencial do escoamento de amônia são desprezíveis! Logo os termos de energia cinética e energia potencial não estão presentes na fórmula. No entanto, ao contrário da primeira lei para compressores, a taxa de troca de calor está presente para ser calculada.
A fórmula acima mostra que precisamos encontrar os valores de e para calcular .
Passo 7
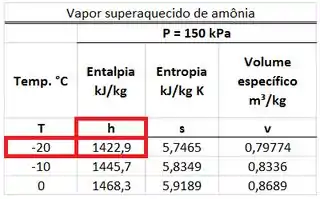
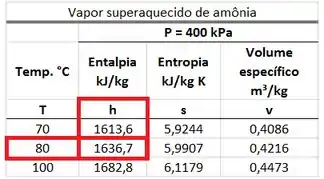
Como a amônia que entra no dispositivo é um vapor superaquecido, temos que procurar o valor da entalpia específica na tabela de vapor superaquecido da amônia. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
Como a amônia que sai do dispositivo é um vapor superaquecido, temos que procurar o valor da entalpia específica na tabela de vapor superaquecido da amônia. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
Tendo todos esses valores, podemos começar nossas contas!
Passo 8
Esse resultado não possui o sinal de ainda. Como é negativo, precisamos colocar um sina lde menos no valor acima.
Substituindo esse valor na fórmula de , encontramos: