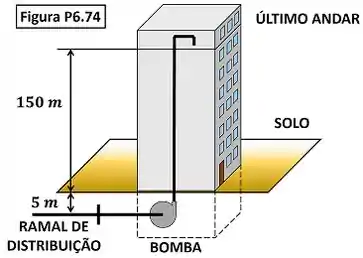
A pressão e a temperatura da água que escoa no ramal de distribuição do edifício mostrado na Fig. P6.74 são iguais a e . O ramal está localizado num plano localizado a do chão e a pressão da água na tubulação localizada no andar superior deve ser igual quando a vazão em massa for igual a . Admitindo que as variações de energia cinética dos escoamentos são desprezíveis e que o escoamento é isotérmico, determine a potência necessária para acionar a bomba.
Passo 1
O exercício pede para a gente calcular a potência necessária para acionar a bomba. A diferença desse exercício para um exercício mais simples de bomba é que nesse a gente não analisa só a bomba. Nessa questão a gente vai estudar a bomba mais a tubulação que leva água até o último andar do prédio. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
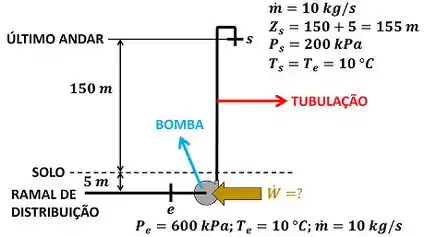
é a vazão mássica de água entrando e saindo da bomba e da tubulação. é a temperatura da água entrando na bomba e é a temperatura da água saindo da tubulação. é a pressão da água entrando na bomba e é a pressão da água saindo da tubulação. é a altura da saída da tubulação em relação ao ramal de distribuição. é a potência que a bomba consome para funcionar.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em uma bomba em regime permanente. Mas cuidado! O enunciado nos informa a altitude da seção de descarga da tubulação. Isso significa que a forma da primeira lei que precisamos usar tem que levar em conta o termo de energia potencial da água que está saindo da tubulação . Mas CUIDADO! Precisamos dividir essa energia potencial por mil para passar a unidade desse termo de para .
Para calcular , precisamos encontrar os valores das entalpias específicas da água entrando na bomba e da água saindo da tubulação . Nós vamos aprender a fazer isso nos próximos passos!
Passo 3
A água entrando na bomba é um líquido comprimido porque a sua pressão de é maior que a pressão de saturação dessa substância a . Por isso, nós teríamos que procurar o valor da entalpia específica na tabela de líquido comprimido da água. No entanto, não existe tabela de líquido comprimido da água para uma pressão tão baixa.

Por isso, vamos ter que aproximar a entalpia específica da água líquida comprimida a como a soma entre a energia interna da água líquida saturada a e .
onde é o volume específico da água entrando na bomba.
Se considerarmos que a massa específica da água possui um valor típico de , pode ser encontrado.
O valor de está na tabela de saturação, na mesma linha da temperatura de e na mesma coluna que . No entanto, nós não vamos precisar desse valor. O motivo será explicado no próximo passo.
Passo 4
Nós também vamos aproximar como a soma entre a energia interna da água líquida saturada a e .
onde é o volume específico da água saindo da tubulação.
Se considerarmos novamente que a massa específica da água possui um valor típico de , pode ser encontrado.
Ou seja, usamos a mesma aproximação para e . Logo, os dois são iguais e serão cortados da primeira lei.
Com essa nova fórmula, podemos iniciar as contas!
Passo 5
O fato desse valor estar negativo apenas indica que a bomba está sofrendo trabalho. Ou seja, ela está recebendo potência.