O compressor de uma turbina a gás de grande porte recebe ar do ambiente a uma velocidade baixa e a e . Na saída do compressor, o ar apresenta pressão igual a , temperatura de e velocidade de . Sabendo que a potência de acionamento do compressor é igual a , determine a vazão em massa de ar que escoa na unidade.
Passo 1
Não se assuste! Por mais que o enunciado fale de turbina, a questão é de apenas um equipamento: o compressor. O exercício pede para a gente calcular a vazão mássica que passa pelo compressor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
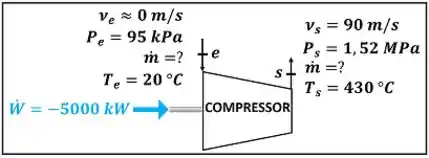
é a vazão mássica do ar entrando e saindo do compressor. e são as temperaturas do ar entrando e saindo do compressor respectivamente. e são as temperaturas do ar entrando e saindo do compressor respectivamente. e são as velocidades do ar entrando e saindo do compressor respectivamente. é a potência que o compressor consome para funcionar.

Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa!
Ela é negativa, porque o compressor está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em um compressor em regime permanente. Mas cuidado! O enunciado nos informa a velocidade do ar saindo do compressor e diz que a velocidade do ar entrando no compressor é baixa . Isso significa que a forma da primeira lei que precisamos usar tem que levar em conta o termo de energia cinética do ar saindo do compressor . Mas tenha atenção! Precisamos dividir essa energia cinética por mil para passar a unidade desse termo de para .
A diferença de entalpia do ar possui uma fórmula em função do calor específico a pressão constante do ar.
Substituindo essa fórmula na primeira lei, encontramos uma fórmula para .
Tendo toda essa informação em mãos, vamos iniciar as contas no próximo passo!
Passo 3
O valor de do ar em que vamos usar na primeira lei vale:
Substituindo esse valor na fórmula, encontramos: