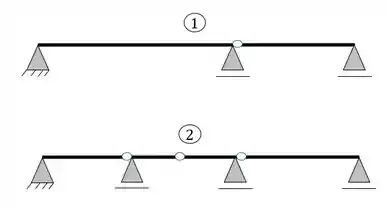
Abaixo são dados dois exemplos de vigas estruturais.
Com base em seus conhecimentos defina se essas estruturas são Isostáticas, hiperestáticas ou ainda hipostáticas. Caso as estruturas sejam definidas como os dois últimos casos antes mencionado, determine maneiras de transformamos elas em estruturas isostáticas.
Passo 1
Fala aí, galerinha. Vamos começar definindo nossas vigas!!!
Pra saber se uma estrutura é isostática, hipostática ou hiperestática, nós precisamos calcular o número de equações e o número de incógnitas. A equações são as equações de equilíbrio. E as incógnitas são as reações de apoio da nossa estrutura.
Se o número de incógnitas é MENOR que o número de equações, a estrutura é HIPOSTÁTICA!
Se o número de incógnitas é IGUAL ao número de equações, a estrutura é ISOSTÁTICA!
Se o número de incógnitas é MAIOR que o número de equações, a estrutura é HIPERESTÁTICA!
Na nossa estrutura 1, temos 2 incógnitas referentes ao apoio de segundo gênero e, para cada apoio de primeiro gênero, temos mais 1 incógnita. Então ao todo temos 4 incógnitas (reações de apoio). Como sempre, nós temos 3 equações da estática, mas, nesse caso, teremos mais 1 por causa da rótula. Para cada rótula, ganhamos mais 1 equação, pois o somatório de momentos na rótula é igual a zero. Então isso quer dizer que temos o mesmo número de equações e incógnitas, ou seja, nossa estrutura 1 é ISOSTÁTICA!
Na nossa estrutura 2, temos 5 reações de apoio (2 do apoio de segundo gênero e mais 1 pra cada apoio de primeiro gênero). E como temos 3 rótulas, vamos ter mais 3 equações além das 3 equações de equilíbrio. Então ao todo temos 5 incógnitas e 6 equações, esse é um caso de estrutura HIPOSTÁTICA!
Passo 2
A questão também pede pra gente dizer formas de transformar as vigas hipostáticas ou hiperestáticas em vigas isostáticas. Pra primeira, não vamos precisar. Vamos ver como vai ficar isso pra segunda!
Na verdade, isso é bem simples. Uma forma de aumentar o número de incógnitas é transformar os apoios. Na figura abaixo trocamos o apoio mais à direita, que era de primeiro gênero, por um apoio de segundo gênero. Mas também poderíamos ter trocado um dos apoios centrais, em vez desse último. Também poderíamos ter trocado o apoio de segundo gênero por um engaste e deixar os de primeiro gênero como estão, porque o apoio de terceiro gênero tem 3 reações de apoio e então elas totalizariam 6 incógnitas.

Em vez de aumentar o número de incógnitas também podemos diminuir o número de equações. E o jeito de fazer isso é retirando rótulas. Como só temos uma equação a mais que o número de incógnitas, tiramos a rótula do meio. Mas poderíamos ter tirado qualquer uma das 3 que também daria certo.

Essa forma de resolver, trocando apoios e rótulas também pode ser usado para as estruturas hiperestáticas. Mas aí fica ao contrário. Nas hiperestáticas, vamos adicionar rótulas (pra aumentar o número de equações) ou quebrar vínculos dos apoios transformando em apoios mais simples (para diminuir o número de incógnitas). Você vai ver muito disso mais pra frente no assunto de estruturas hiperestáticas!
Resposta
A viga 1 é isostática.
A viga 2 é hipostática. Para transformá-la em isostática podemos retirar 1 rótula ou trocar 1 dos apoios por uma opção mais restritiva.