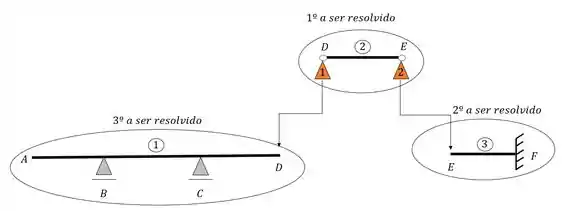
Paras a viga Compostas abaixo, faça a separação correta em vigas simples indicando onde ficaram os apoios fictícios e para onde serão transferidas as suas reações de apoios.

Passo 1
Sempre que estivermos em um caso de separação de vigas, devemos fazer o seguinte
- Primeiro e mais importante, devemos fazer a separação SEMPRE quebrando nas rótulas, nunca, em outros trechos.
- Quando quebrar uma rótula deve-se analisar o seguinte, o apoio fictício que aparece nela, terá para onde transferir essa reação e manter a estrutura que ele está isostática? Se a resposta for sim, então cortamos a rótula corretamente, se for não, provavelmente escolhemos a estrutura errada, ou, de fato, essa rótula não pode ser retirada.
- Analisamos se todas as estruturas são isostáticas, se forem, a separação está correta, se não forem devemos ver o seguinte. Ou a separação foi feita errada, ou, a estrutura não é isostática
- Por fim, analisamos a ordem de solução da nossa viga, o que facilita na hora de fazer os cálculos.
Entendido isso, podemos ir para o exercício, para colocarmos em pratica o nosso passo a passo. Vamos lá? Sigam-me os Bons!!

Passo 2
Vamos lá então, como vimos, precisamos quebrar as rótulas, e avaliar quais seriam as barras mais aptas a receberem os apoios fictícios, e qual barra se apoia em qual, vamos fazer isso então, quebrando as rótulas teremos que

Sabemos então que agora temos barras separadas, e elas ficaram separadas da seguinte maneira, e com os seguintes nomes
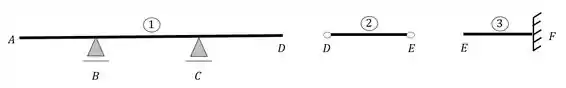
Mas como escolher os apoios fictícios?
O macete é ver quem já está equilibrado e descartar, nesse caso as vigas 1 e 3 já são auto equilibradas, pois a viga 1 tem 2 incógnitas e 2 equações, lembrando que como se trata de vigas descartamos os esforços horizontais, assim como a viga 3 que também tem 3 incógnitas e 3 equações, ou seja, nos trechos que quebramos as suas rótulas não colocaremos apoios fictícios.
Porém veja que a barra 2 não está equilibrada, e ela possui rótulas que quebramos, com isso, será mais usual colocar os apoios fictícios nelas.
Passo 3
Colocando os apoios fictícios na barra 2, onde quebramos as rótulas e numerando os apoios fictícios, teremos,
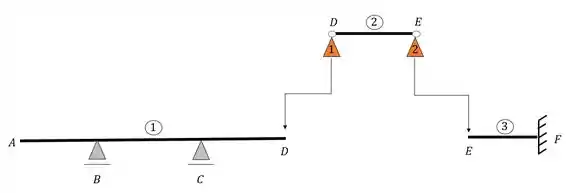
Perceba o seguinte, a viga 2 passou a ser estável, se tornando isostática quando analisamos ela com o apoio fictício.
Também devemos ver o seguinte
- Apoio 1 transfere suas reações, com sinal invertido, para a viga 1
- Apoio 2 transfere suas reações, com sinal invertido, para a viga 3
Passo 4
Veja que seguimos o nosso passo a passo,
- Primeiro quebramos as rótulas e separamos as vigas.
- Depois avaliamos onde ficariam os apoios fictícios e vimos que todas as rótulas foram cortadas corretamente.
- No final do segundo passo, avaliamos se todas as estruturas eram isostáticas, e de fato eram.
Agora só falta o último passo:
Definir a ordem de solução, e essa ordem é bem simples, basta ver o seguinte, quem tem apoio fictício, sempre é resolvido primeiro, quem recebe as reações dos apoios fictícios, são resolvidas posteriormente, com isso teremos a seguinte ordem de solução
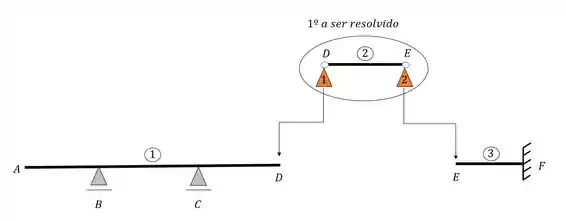
Tendo em mãos todas as reações de apoio fictício, transferimos elas para as suas barras corretas, seguindo a ordem do final do passo 2. Tomar cuidado pois essas reações vão para as suas barras correspondentes com os sinais invertidos, ou melhor, o sentido dos vetores calculados será contraria a direção calculada, feito isso, a próxima sequência de solução será
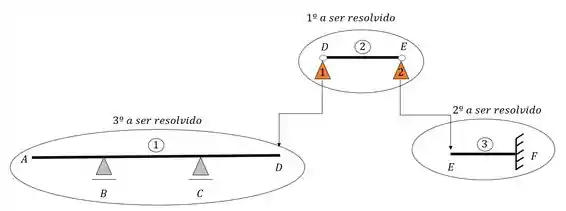
E com isso cumprimos o que foi pedido no exercício. Separamos as vigas, conferimos se todas são isostáticas, colocamos os respectivos apoios fictícios, e por fim definimos a ordem de solução. Show? Vamos para o próximo exercício então.
Resposta
As vigas separadas e a ordem de solução será