Dada a tensão senoidal , determine:
- A amplitude ;
- O período ;
- A frequência ;
- em ;
Passo 1
Vamos pegar a expressão da forma de onda da tensão:
E retirar as informações de acordo com o modelo:
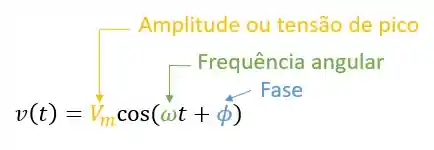
Comparando a expressão com o modelo, descobrimos que:
- A amplitude é igual a
- A frequência angular é igual a
- A fase é igual a
Passo 2
Então já respondemos a letra “a”, a amplitude é igual a:
Passo 3
A partir da frequência angular:
Vamos descobrir a frequência em , através da equação:
Substituindo a frequência angular:
Vamos isolar a frequência de um lado da igualdade:
Passo 4
Agora que já temos a frequência , podemos encontrar o período simplesmente fazendo a inversão:
Vamos logo substituir a frequência que encontramos:
Encontramos logo o período igual a:
Não esquece da unidade em segundos!
Passo 5
Para encontrar a tensão no tempo , vamos substituir esse valor de tempo na expressão da tensão:
Substituindo o tempo
Na expressão:
Realizando essa multiplicação:
Nós não podemos apenas somar os argumentos que estão dentro do cosseno, porque estão em unidades diferentes. Um está em graus e outra em radiano.
Vamos converter para grau. Para isso temos que multiplicar por :
Então a expressão se torna:
Somando as parcelas dentro do cosseno:
Calculando o cosseno de
Substituindo esse resultado na expressão do cálculo da tensão que estamos fazendo:
Chegamos ao resultado:
Acabou a questão! Chegamos aos resultados!