Dado e , determine o ângulo de fase entre as duas senoides.
Passo 1
Para comparar duas ondas, precisamos que elas estejam em função de cosseno ou de seno, não podemos comparar duas formas de expressão diferentes. Então precisamos passar a expressão:
Para a forma de cosseno, como já está ! É mais comum trabalhar com formas de onda na forma de cosseno.
Lembra a regra para transformar de seno para cosseno? Vou relembrar aqui.
Caso o sinal que acompanha o seno for negativo, somaremos ao ângulo do seno para transformar em cosseno:
Caso o sinal que acompanha o seno for positivo, subtrairemos ao ângulo do seno para transformar em cosseno:
No nosso caso, a expressão:
Tem como número que acompanha o , ou seja, é positivo. Dessa forma devemos subtrair :
Passando a expressão para cosseno:
É igual a:
Fazendo essa subtração dentro do cosseno:
Chegamos a expressão final:
Passo 2
Então temos as duas expressões agora:
Você está estranhando esses ângulos negativos, eu também prefiro trabalhar com ângulos positivos, então podemos somar ao ângulo, porque dessa forma obtemos a forma positiva e não alteramos a direção.
Somando nas duas expressões de tensão:
As somas dentro dos cossenos:
Logo, ficamos com as expressões:
Passo 3
O módulo da tensão é , enquanto o módulo da tensão é :
O ângulo de fase da tensão é , enquanto o módulo da tensão é :
Podemos escrever as tensões como fasores, dessa forma:
Colocando essas duas tensões em um diagrama fasorial, vamos considerar apenas o módulo e o ângulo.
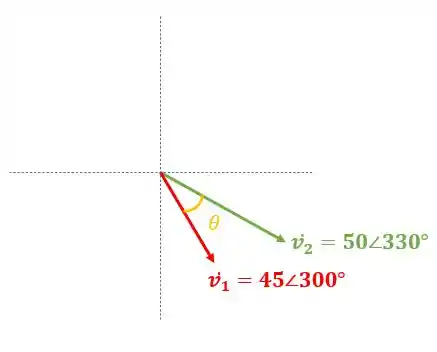
Nós queremos encontrar o ângulo de fase entre os dois fasores. Nada mais é que subtrair um ângulo do outro:
Logo o ângulo de fase é igual a:
Essa é a resposta que ele tanto queria!