Caracterize a cônica representada por cada uma das equações abaixo e faça seu gráfico:
a)
b)
Passo 1
- Bom, primeiramente vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
- Vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
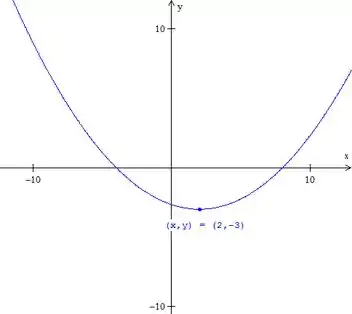
Perceba que apenas a variável está elevada ao quadrado. Desconfiamos de um parábola.
Passo 2
Arrumando a equação temos:
Vamos coloca-la na forma geral da parábola:
Ajeitando os quadrados fica:
Que é exatamente a equação da parábola com vértice em e foco
Passo 3
Para fazer seu esboço primeiro perceba que a variável elevada ao quadrado é . Marque o vértice. Fica:
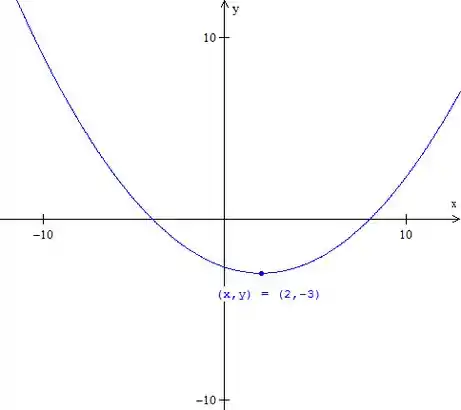
Passo 4
Que é o mesmo que:
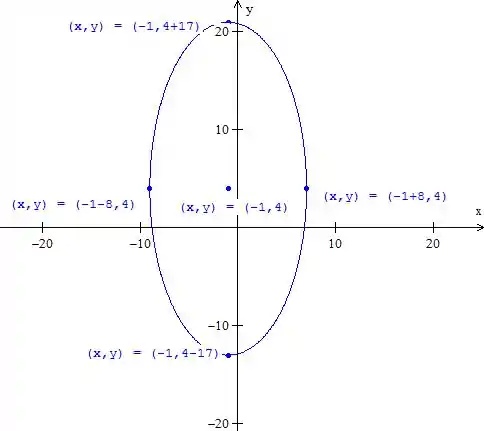
Temos dois termos elevados ao quadrado de mesmo sinal. Desconfiamos de uma elipse ou circunferência.
Passo 2
Vamos coloca-la na forma:
Completando os quadrados temos:
Completando os quadrados de temos:
Passo 3
Substituindo na equação temos:
Ajeitando:
Que é a equação da elipse com centro em e semieixos e
Passo 4
Para fazer o gráfico, marcamos o centro e os semieixos:
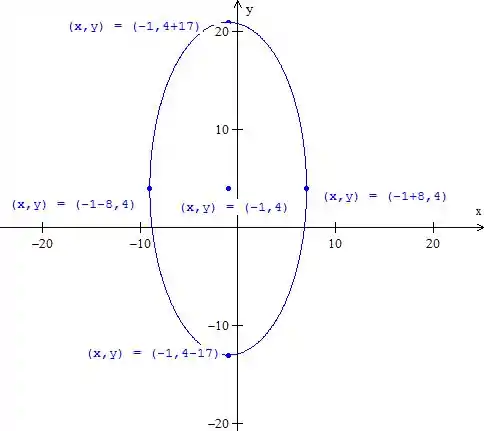
Resposta
- Parábola com vértice em e foco
- Elipse com centro em e semieixos e