Caracterize a cônica representada por cada uma das equações abaixo e faça seu gráfico:
a)
b)
c)
Passo 1
- Bom, primeiramente vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
- Bom, primeiramente vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
- Bom, primeiramente vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
Perceba que tanto quanto estão elevados ao quadrado e os seus sinais são iguais (ambos positivos).
Passo 2
Das cônicas que vimos na teoria, apenas a circunferência e a elipse tinham as duas variáveis elevadas ao quadrado e com o mesmo sinal. Provavelmente, a cônica dada nessa questão será uma delas.
Para provar isso, vamos ajustar a equação dada completando os quadrados. Vamos começar ajustando os termos dependentes de . Temos:
Podemos colocar o em evidência:
Vamos agora completar os quadrados da parte de dentro dos parênteses.
Perceba que nos faz lembrar . A única diferença é que esse “+4” aí não aparece. Podemos ajustar. Temos:
Eu apenas somei 4 e subtraí 4 dentro dos parênteses. Agora, temos o seguinte:
Ou seja:
Passo 3
Desenvolvendo o mesmo raciocínio para os termos dependentes de temos:
Colocando em evidência:
O termo nos faz lembrar . Podemos fazer o seguinte:
Ou seja:
Passo 4
Substituindo na equação da cônica dada temos:
Ajeitando a equação:
Chegamos então à:
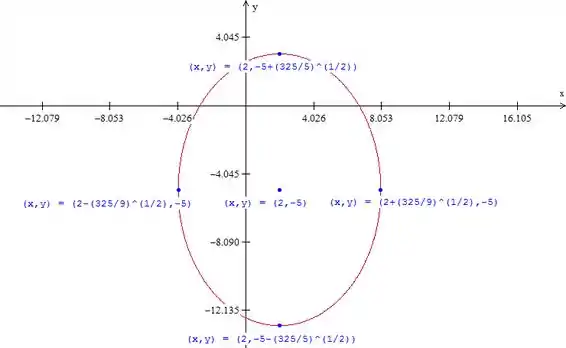
Que é a equação de uma elipse com centro em e semieixos e .
Passo 5
Vamos fazer seu gráfico. Marcamos o centro e os semieixos e desenhamos a elipse. Fica:
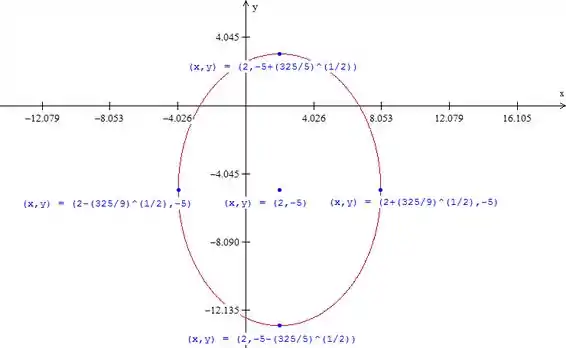
Passo 6
Perceba que tem grau 1 porém aparece com grau 2. Desconfiamos fortemente de uma parábola.
Passo 7
Arrumando a equação temos:
Vamos colocá-la na forma geral da parábola:
Ajeitando os quadrados fica:
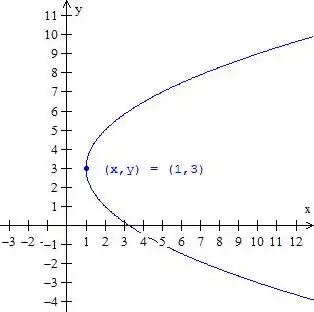
Que é exatamente a equação da parábola com vértice em e foco
Passo 8
Para fazer seu esboço primeiro perceba que a variável elevada ao quadrado é . Marque o vértice. Fica:
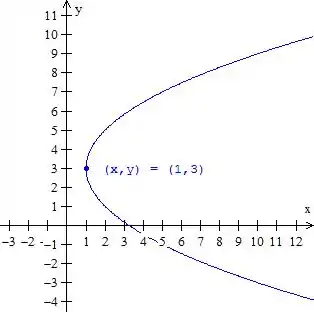
Passo 9
Perceba que tanto quanto estão elevados ao quadrado porém seus sinais são opostos. Desconfiamos de uma hipérbole.
Passo 2
Vamos tentar colocar essa equação na forma:
Ou
Vamos ajeitar os quadrados referentes a variável :
Passo 3
Fazendo o mesmo para a variável temos:
Passo 4
Substituindo na equação:
Tem de aparecer do lado direito, então vamos dividir tudo por :
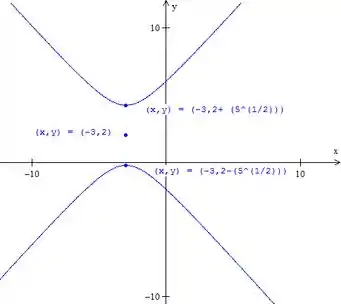
Portanto a equação é uma hipérbole com centro em e vértices em e .
Passo 5
Para fazer seu gráfico, marcamos o centro e os vértices. Fica:
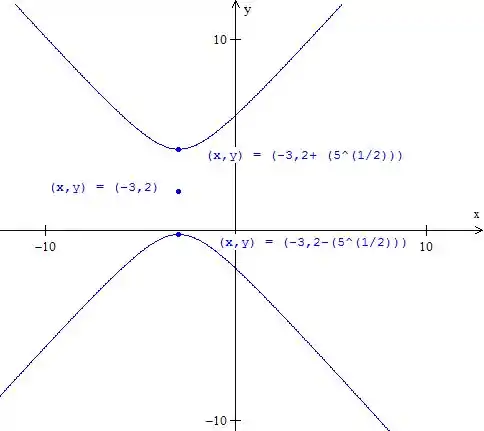
Resposta
- Elipse com centro em e semieixos e .
- Parábola com vértice em e foco
- Hipérbole com centro em e vértices em e