Uma bola de a uma velocidade de atinge uma mola de constante elástica igual a que sofre uma compressão de . Calcule a constante elástica da mola.
Considere .
Passo 1
Preparados para mais uma questão de conservação de energia?? Então bora!!
Vamos começar entendendo o que está acontecendo pelo desenho
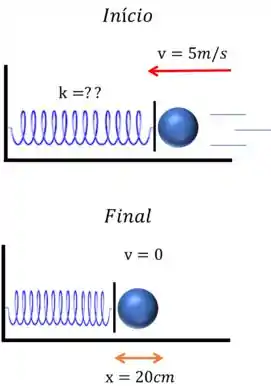
Vamos conservar a energia do movimento da bola!
E a energia mecânica é a soma das energias cinética com a potencial de um corpo em certo momento
E só lembrando aqui rapidinho, temos que a energia cinética é dada por
E a energia potencial é separada pela energia potencial gravitacional e a energia potencial elástica.
Cada uma delas é calculada desse jeitinho aqui
Show, agora que já relembramos uns conceitos importantes vamos começar de fato o problema.
OBS: Podemos usar a energia potencial tanto com a letra quanto com , cada livro escreve de uma forma e cada professor escolhe a que acha melhor. Aqui usaremos sempre a notação com , ok? 😊
Passo 2
Como no nosso exercício a bola está sempre na mesma altura, então não haverá energia potencial gravitacional em nenhum momento
Que maravilha! Menos uma coisa para nos preocuparmos hehe. Vamos analisar apenas as energias cinética e potencial elástica.
Observem o momento antes da bola atingir a mola.
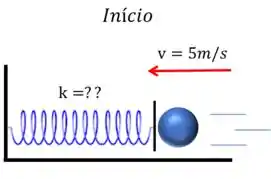
Nesse instante ela tem uma velocidade de , então existe uma energia cinética envolvida nesse movimento. Se a energia cinética tem a fórmula:
Podemos substituir os valores dados no enunciado:
Encontraremos:
Elevando o ao quadrado, temos:
Agora fazendo a multiplicação do numerador
E finalmente fazendo a divisão
Encontramos a energia cinética inicial, mas quanto vale a energia potencial elástica inicial?
Passo 3
Como nesse momento a bola acabou de chegar na mola, ainda não deu tempo de começar a comprimi-la, então podemos considerar que a mola está sem nenhuma deformação
Como a energia potencial elástica é igual a:
Nós não sabemos a constante elástica da mola , mas sabemos que a deformação é nula, então vamos substituir:
Sabemos que qualquer número multiplicado por zero é igual a zero, então a energia elástica armazenada inicialmente na mola é igual a zero!
Passo 4
Sabendo tanto a energia cinética inicial quanto a energia potencial elástica inicial, podemos descobrir o valor da energia mecânica inicial:
Substituindo os valores que já sabemos:
Sobre a energia potencial gravitacional nós já conversamos no Passo, por ela ser zero nesse exercício, nem precisamos escrever, beleza?
Passo 5
Após a bola atingir a mola, a velocidade vai diminuindo até chegar a zero, isso ocorre quando a mola chegou no seu limite de deformação .
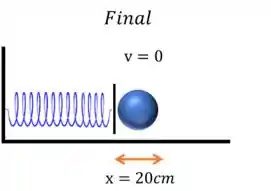
Então no final, a energia cinética será:
Podemos substituir os valores dados no enunciado e que encontramos:
Encontraremos:
Logo a energia cinética final é igual a zero, pois a velocidade final é igual a zero!
Passo 6
Se já encontramos que quando a deformação da mola é máxima, a energia cinética é zero, quanto vale a energia potencial elástica? A energia potencial elástica é igual a:
Substituindo os valores finais:
Não esquece de passar a unidade de centímetros para metros! Então a energia potencial elástica final é igual a:
Elevando ao quadrado:
Sim, nós não temos ideia de quanto vale a constante , é exatamente ela que queremos calcular! Então vamos deixar ela quietinha aí.
Vamos só fazer a simplificação do por
Passo 7
Logo, a energia mecânica final total é igual a:
Substituindo os valores das energias que encontramos:
Passo 8
Vamos conservar a energia? Então vamos igualar a energia mecânica inicial e final:
Substituindo os valores que encontramos:
Para encontrar o , vamos passar o para o outro lado dividindo
Realizando essa divisão:
Encontramos o valor final da constante elástica da mola!